Il SISTEMA METRICO DECIMALE

Le occorrenze de' tempi in cui viviamo mette ogni individuo quasi in obbligo stretto di procacciarsi una sufficiente cognizione del sistema metrico decimale. Sistema il quale conosciuto di grande utilità e di vantaggio universale fu con legge approvato e verrà posto in vigore negli Stati nostri nel 1850.

Ognuno facilmente capisce in quante maniere si può andar soggetto ad errore, a frode, è talvolta a non lieve danno in un pressochè totale cangiamento di pesi e di misure.

Desideroso io di prevenire tali inconvenienti e di giovare per quanto posso al pubblico bisogno ho compilato il presente libretto, il cui scopo si è di ridurre il sistema metrico alla massima semplicità per modo che una persona mediocremente culla lo possa capire leggendo anche senza aiuto del maestro.

Per essere più facilmente capito alcune volte ho trasandato la proprietà della lingua aritmetica premendomi assolutamente di essere inteso e non più. {3 [3]}

Le opere dei chiari professori Giulio, Milanesio, Borghino, il trattato di aritmetica stampato da un Fratello delle Scuole cristiane, mi servirono di norma.

Per la cognizione del nuovo sistema essendo di tutta necessità le quattro prime operazioni dell'aritmetica; queste si fecero brevemente precedere nel modo che potranno servir di base a tutte le operazioni del nuovo sistema. Seguirà uno specchio in cui si pongono le misure ed i pesi antichi a fronte de' pesi e delle misure che verranno sostituite col reciproco loro rapporto. Applicando poscia le quattro anzidette operazioni alla nuova nomenclatura metrico-decimale si perverrà alla reciproca riduzione delle misure e de' pesi del sistema antico col nuovo colla semplice moltiplicazione.

Questa seconda edizione venne migliorata ed accresciuta di più cose suggerite dalla pratica, e giudicate di tutta necessità per la cognizione e semplificazione del nuovo sistema.

Mio scopo è di presentare al pubblico un compendio semplice e chiaro, e adattato alla capacità di ogni leggitore; che se le mie deboli fatiche non potranno tutti appagare saranno almeno degne di benigno compatimento. Si provi ogni cosa e si ritenga ciò che pare più buono. {4 [4]}

[Le quatro operazioni]

Dialogo

D. Che cosa è l'aritmetica?

R. L'aritmetica è la scienza de' numeri.

D. Che vuol dire numero?

R. Numero vuol dire unione di più unità.

D. Che vuol dire unità?

R. Unità vuol dire una cosa sola o considerata come sola, p. e. un libro, un calamajo, un bicchiere una tavola ecc.

D. Quali sono le operazioni fondamentali dell'aritmetica?

R. Le operazioni fondamentali che formano la base di tutta l'aritmetica sono l'addizione, la sottrazione, la moltiplicazione, la divisione. Ma prima di fare queste operazioni convien conoscere i numeri.

Regole per conoscere i numeri

D. Quanti sono i numeri?

1	2	3	4	5	6	7	8	9	0
uno	due	tre	quattro	cinque	sei	sette	otto	nove	zero
.	..	…	….	…..	……	…….	……..	………

Lo zero per se non significa niente; e serve solamente a rimpiazzare le altre cifre od accrescerne il valore.

D. E quando ci sono più di nove unità?

R. Quando le unità oltrepassano il nove si conterà nel modo seguente: {5 [5]}

La prima cifra esprime le unità e	1	uno
Seconda le decine	12	dodici
Terza le centinaia	123	cento ventitrè
Quarta unità di mila	1234	mille dugento trentaquattro
Quintale decine di mila	12345	dodicimila trecento quarantacinque
Sesta le centin. di mila	123456	cento ventitrè mila quattrocento cinquantasei
Settima le unità di milioni	1234567	unmilione ducento trentaquattro mila cinquecento sessantasette
Ottava le dee. di mil	12345678	dodici milioni trecento quarantacinque mila seicento settantotto
Nona le centinaia di milioni	123456789	cento ventitrè milioni quattrocento cinquantasei mila settecento ottanta nove
Decima le unità di bilioni ecc.	1234567890	un bilione ducento trentaquattro milioni cinquecento sessantasette mila ottocento novanta

Esercizi sulla numerazione.

Si scriva in cifre diciassette franchi. Cento venticinque giovani virtuosi. Mille ducento tegole.

La città di Torino conta circa cento quaranta mila abitanti. {6 [6]}

Dell'addizione.

D. Che cosa è l'addizione?

R. L'addizione c l'unione di pio numeri della medesima specie per vedere presi insieme quanto formino.

I numeri che si devono unire si dicono poste.

Il numero che risulta dall'unione delle poste si appella somma o totale.

D. Non si possono unire insieme i numeri di specie diversa?

R. I numeri di specie diversa non si possono unire insieme; perciò se io dico: 25 franchi 50 rubbi bisogna considerare le somme separatamente. Se poi dico: 25 fr. 50 fr. si Eossono unire insieme perché sono della medesima specie.

D. Che cosa bisogna osservare intorno all'addizione?

R. Per fare l'addizione bisogna osservare attentamente che le cifre delle varie poste vengano scritte in maniera che le unità siano scritte sotto alle unità, le decine sotto alle decine, le centinaia sotto alle centinaia ecc.

Esemp. dovendo scrivere 543 e 95 si disporranno i numeri così:

Prima posta	543
Seconda posta	95

Nel che dobbiamo badare che il numero 5 venga scritto sotto al 3; il 9 sotto al 4.

Disposti così i numeri e tirata una linea orizzontale si farà l'operazione nel modo seguente: {7 [7]}

Prima posta	543
Seconda posta	95
Linea orizzontale	____
Totale	638

Si comincierà dalla colonna delle unità dicendo: 5 e 3 dà 8, e scriveremo 8. Poi si passa alla colonna delle decine dicendo: 9 e 4 fanno 13, e scritto 3 si porterà una decina nella colonna dicendo: 1 e 5 fanno 6. Il totale sarà 638.

Qui convien notare che se i numeri della stessa colonna presi insieme fanno dieci si scriverà 0 nella colonna delle unità e si porterà uno nella colonna delle decine. In generale, nel sommare più numeri quando oltrepassano il dieci si metterà solamente l'ultima cifra de' numeri da sommarsi, e le decine considerate come unità verranno trasportate nella colonna che segue:

Esempio

Prima posta	389
Seconda posta	154
Terza posta	392
Linea	___
Totale	935

Cominciando dalla posta superiore Si dirà: 2 e 4 fanno 6, più 9 danno 15, si scriverà 5 sotto alle unità e si trasporterà uno nella colonna delle decine dicendo: 1 e 9 fanno io, più 5 danno 15, più 8 eguagliano 23. Si scrive 3 sotto alla colonna delle decine e si porterà 2 nella colonna dei centinaja (questi due eguagliano venti decine ovvero ducento), indi si continuera: 2 e 3 fanno 5, più 1 fa 6, più 3 fa 9. Il totale sarà 935.

D. Come si fa la prova dell'addizione?

R. La prova dell'addizione si fa sommando il totale colle poste de' numeri e prendendo la metà della somma totale. Se questa metà eguaglia il primo totale l'operazione è esatta. {8 [8]}

Esempio	634
	428
	____
Primo totale	1936
	____
Prova	3872
Si prende la metà	____
del secondo totale	1936

Per dividere l'ultimo totale per metà si dirà: la metà di 3 è 1 col residuo di 1, il quale posto a sinistra dell'8 fa 18. La metà di 18 è 9. La metà di 7 è 3 col residuo di 1 che posto a sinistra del 2 fa 12. La metà di 12 è 6. Questa metà (1936) corrispondendo al primo totale l'operazione è esatta.

Esercizi sull'addizione.

1. Un padrone pagò fr. 750 per 6tto di bottega. Più 160 per stipendio annuo a due operai. Più 130 ad un apprendizzo che aveva mostrato speciale diligenza nel servirlo. Quanto ha speso in tutto?

2. Un falegname ha speso in assi fr. 526; in travi 847; in comperare utensili 235. Quanto ha speso in tutto?

3. Un contadino ha speso per la propria famiglia in abiti fr. 300; in fromento 150; in meliga 367. Quanto ha speso in tutto?

Della sotrazione

D. Che cosa è la sottrazione?

R. La sottrazione è un'operazione per cui si leva una somma minore da una somma maggiore ovvero eguale per conoscere quanto resti. Dicesi comunemente deve paga. {9 [9]}

D. Quali nomi soglionsi usare nella sottrazione?

R. Il numero maggiore che si vuole diminuire appellasi minuendo; il minore, che si vuole levar dal maggiore dicesi sottraendo; quello che resta si nomina residuo.

D. Come si fa la sottrazione?

R. Per fare la sottrazione si scrivono le unità e le altre cifre del sottraendo sotto a quelle del minuendo, e tirata una linea si comincia dalla destra a sottrarre le unità, e le decine dalle unità e dalle decine, scrivendo il residuo al di sotto della linea: lo stesso si farà colle altre cifre andando verso sinistra finchè sia finita l'operazione.

Esempio. Un padre paga 525 franchi di pensione per un figlio, ne ha già pagato 313; quanto deve ancora pagare?

Operazione.

Deve o Minuendo	525
Paga o Sottraendo	313
Linea orizzontale	___
Residuo	212

Per fare questa operazione si levano 3 da 5; oppure si dirà chi di 5 paga 3 restano 2, i quali scriviamo sotto alla linea. Chi di 2 paga i resta i che porrai pure setto alla linea. Chi di 5 paga 3 restano 2. Il residuo saranno fr. 212.

D. Che cosa bisogna osservare intorno alla sottrazione?

R. Per capire i vari casi della sottrazione bisogna osservare: i. che quando la cifra del sottraendo è uno 0, oppure è uguale alla cifra corrispondente del minuendo, scriveremo 0 sotto alla linea. 2. Quando {10 [10]} la cifra del sottraendo è maggiore del minuendo allora si prenderà una unità dalla prossima cifra del minuendo a sinistra, la quale unità essendo una decina relativamente al posto ove si porta avrà il valore di dieci.

Esempio. Un signore comperò un podere che costò 3405, ne ha già pagato 1605. Quanto deve ancora pagare?

Operazione.

Deve oppure minuendo	3405
Paga oppure sottraendo	1605
Linea orizzontale	_____
Residuo	1800

L'operazione si farà così; 5 meno 5 resta nulla, si scrive 0 nel residuo. 0 meno 0 resta 0, si scrive 0 nel residuo. 4 meno 6 oppure chi di 4 paga 6 paga troppo, perciò si prende una unità dal 3 che unendo al F resta decina onde risulterà 14, 14 meno 6 resta 8; scriviamo 8 nel residuo. Ora dal 3 avendo preso i resta 2; e si dirà 2 meno i resta i. Il residuo sarà: 1800.

D. Come si fa la sottrazione quando s'incontra uno 0 più 0 nel minuendo?

R. Quando nel sottraendo c'è una cifra significativa e nel minuendo s'incontra un 0, allora lo 0 si conta come dieci e la prima cifra elle s'incontra a sinistra diminuisce di uno. Se poi occorrono più 0 uno dopo l'altro si terrà questa regola. Il primo 0 si conta per dieci, gli altri si contano solamente per nove; ma la prima cifra significativa che seguirà a sinistra diminuirà di uno.

Esempio. Un panattiere ha la somma di fr. 3500, {11 [11]} ha già speso in frumento fr. 1327. Quanto ha ancora?

Minuendo	3500
Sottraendo	1327
	_____
Residuo	2173

D. Come si fa la prova della sottrazione?

R. Per fare la prova della sottrazione si somma il residuo col sottraendo, se la somma totale risulta eguale al minuendo l'operazione è esatta.

Esempio. Un impresaro deve provvedere 20550 mattoni, ne ha già provveduto 12500. Quanti ne deve ancora provvedere?

Operazione.

Minuendo	20550
Sottraendo	12500
	______
Residuo	8050
Prova	20550

Esercizi sopra la sottrazione.

1. Un contadino ha il reddito annuo di lire 2650, ne paga 725 per un suo figlio studente all'università, quanto gli resta ancora perla famiglia?

2. La città di Torino in principio dell'anno contava 139246 abitanti, sul finire si trovano registrati nel libro dei morti 4187; quanti rimangono ancora?

3. Un uomo che dovesse vivere sino a 86 anni e 11 mesi, quanto gli rimarrebbe da vivere quando si trova all'età di anni 57, mesi 8? {12 [12]}

Della moltiplicazione.

D. In che cosa consiste la moltiplicazione?

R. La moltiplicazione consiste nel ripetere tante volte un numero detto moltiplicando quante sono le unità di un altro numero detto moltiplicatore.

Il moltiplicando ed il moltiplicatore soglionsi appellare col nome di fattori.

Ciò che risulta dall'operazione dicesi prodotto.

Per imparare la moltiplicazione bisogna esercitarsi alla lettura della tavola seguente:

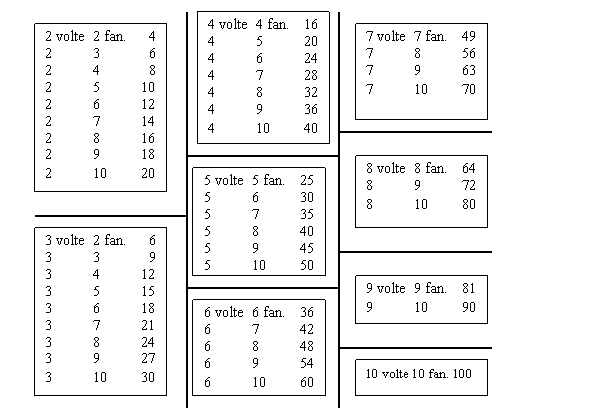
{13 [13]}

D. Come si fa la moltiplicazione?

R. Scritte le unità e le decine del moltiplicatore sotto a. quelle del moltiplicando si tira una linea, indi si prende ciascuna cifra del moltiplicando tante volte, quante sono le unità del moltiplicatore, e quando il prodotto oltrepassa il dieci si scrivono soltanto le unità, e le decine si uniscono al prodotto seguente:

Esempio. Quale prodotto dà 453 moltiplicato per 3.

Operazione.

Moltiplicando	453
Moltiplicatore	3
	____
	1359

Cominciando dalla destra si andrà a sinistra dicendo: 3 volte 3 danno 9 e scriveremo 9 nel prodotto. 3 volte 5 datino 15; porremo 5 che sono unità e si porta una decina nel prodotto seguente. 3 volte 4 danno 12, più uno che abbiamo portato dà 13, che si scrive per intero. Avremo per prodotto 1359.

D. Come si fa la moltiplicazione quando nel moltiplicatore ci sono due cifre, oppure occorrono zeri?

R. Quando nel moltiplicatore ci sono due o più cifre allora si moltiplica ciascuna di esse cifre per tutto il moltiplicando, in modo che ciascun prodotto parziale abbia la sua prima cifra sotto al suo numero moltiplicatore. Poscia si sommano insieme tutti i prodotti. Qualora poi occorrano 0 non si fa altro che scrivere sotto al medesimo un altro 0 nel prodotto.

Esempio. Un agente di campagna spende ogni {14 [14]} giorno in operai fr. 280; quanto spenderà in un anno ovvero in giorni 365?

Moltiplicando	365
Moltiplicatore	280
	______
Primo prodotto	29200
Secondo prod	730
	______
Prodotto totale	102200

Si dirà 0 moltiplicato per 5 dà 0; si scrive 0 nel prodotto sotto allo 0. 8 moltiplicato per 5 dà 40, scriviamo 0 sotto allo stesso 8, e porteremo 4 decine dicendo: 8 moltiplicato per 6 dà 48, più 4 che portavamo danno 52; si scrive s e si portano 5 decine dicendo: 8 moltiplicato per 3 dà 24, più 5 che portavamo danno 29; si depone tutto 29. Il primo prodotto sarà 29200.

Si passa alla terza cifra del moltiplicatore dicendo: 2 moltiplicato per 5 dà 10: si depone 0 nel secondo prodotto, ma sotto al 2; e si porterà tizia decina dicendo: 2 moltiplicato per 6 dà 12, più 1 che portavamo fanno 13; si scrive 3, e si porta una decina dicendo: 2 moltiplicato per 3 dà. 6, più i che portavamo avremo 7. Il secondo prodotto sarà 730; sommando questi due prodotti insieme si avrà il prodotto totale 102200.

D. Come si fa la prova della moltiplicazione?

R. La maniera più semplice e facile per fare la prova della moltiplicazione è quella che io chiamo regola del g. Consiste questa regola nel formare una croce in modo che si trovino quattro angoli.

Nell'angolo superiore a sinistra si porrà la cifra che risulta da tutte le cifre del moltiplicando sommate insieme, ommettendo i 9. {15 [15]}

Nell'angolo inferiore della stessa parte si scriveranno le cifre del moltiplicatore parimenti sommate insieme, ommettendo altresì tutti li 9, p.es.se fosse 23, ommettendo li 9, restano 5. Indi si moltiplicano un per l'altro le cifre dei due angoli, e ciò che oltrepassa il 9 si scrive nell' angolo superiore a destra. Fatto questo si sommano le cifre del prodotto; e ciò che eccede il 9 si scrive nell'angolo inferiore a destra.

Se questa somma eguaglia a quella del suo angolo superiore l'operazione sarà esatta.

Abbiasi a far la prova dell'esempio sovr'esposto.

5 5 1 5	365
	280
	_____
	29200
	730
	______
	102200

Prova. Si sommeranno insieme le cifre del moltiplicando e diremo: 3 più 6 danno 9, più 5 danno 14. Più di 9 è 5 che verrà scritto nell'angolo superiore a sinistra.

Si sommeranno poscia le cifre del moltiplicatore dicendo: 2 più 8 danno 10, più o dà 10. Il più di 9 è 1, che scriviamo nell'angolo sotto al 5.

Qui moltiplicheremo le cifre de' due angoli dicendo: 1 moltiplicato per 5 dà 5, che verrà scritto nell'angolo superiore a destra.

Finalmente si sommeranno tutte insieme le cifre del prodotto dicendo: 1 più 0 dà 1, più 2 dà 3, più 2 fa 5, più 0 sempre 5. Ciò che {16 [16]} risulta non giungendo al 9 scriviamo 5 nell'angolo inferiore a destra. Ora i due angoli a destra avendo cifra pari che è 5, l'operazione è esatta.[1]

Esercizi sulla moltiplicazione.

1. Un padre spende in giuoco e ghiottonerie fr. 7 in ogni domenica; quanto scialacquerà in 52 settimane ovvero in un anno?

2. Un figlio consuma in gozzoviglie e fumare tabacco 2 fr. per settimana, quanto avrebbe infine dell'anno astenendosi da tali vizi?

3. Una madre comperò 219 rasi di panno a fr. 8 il raso; quanto deve pagare?

4. Ogni giorno è di 24 ore, quante ore ci sono in 365 giorni ovvero in un anno?

5. Quanto si deve pagare per 85 brente di vino a fr. 12 la brenta?

6. Quanto si deve pagare per 223 emine di fromento a fr. 5 l'emina?

Della divisione.

D. Che cosa s'intende per divisione?

R. Per divisione non s' intende altro che il {17 [17]} dividere un numero in più parti eguali. Il numero che si vuol dividere dicesi dividendo; quello per cui si divide appellasi divisore; la parte che risulta dicesi quoziente.

D. Come si fa la divisione?

R. Si scrive il dividendo, che viene separato dal divisore per mezzo di una linea orizzontale e di un' altra perpendicolare come nella figura seguente I seguenti esempi insegneranno il modo di fare la divisione.

Un padrone vuole regalare fr. 92 a 4 suoi garzoni per buon capo d'anno; quanto avrà ciascuno?

Dividendo	92	4 divisore
	8	23 quoziente
	___
	12
	12
	___
	00

Scritto il divisore a destra del dividendo come sopra, si osserverà quante volte il divisore stia nella prima cifra del dividendo, e diremo: il 4 nel 9 sta due volte, e si scrive 2 nel quoziente sotto al divisore; per non confondere l'operazione bisogna subito separare il 9 con una virgola per significare che si è preso. Lo stesso si osserverà per tutti gli altri numeri. Quindi si moltiplichi il quoziente 2 pel divisore 4, e avremo 8. Questo 8 si scrive sotto al g del dividendo, e si farà la sottrazione dicendo: 9 meno 8 resta 1, Si proseguirà: il 4 in 1 non istà più, perciò si abbassa un'altra cifra del dividendo che è 2, e si porrà a {18 [18]} destra dell' 1 che farà 12. Ora si dirà: il 4 nel 12 sta tre volte; si metterà 3 nel quoziente a destra del 2 e moltiplicando 3 pel divisore 4, si avranno 12 che scriveremo sotto al 12 del dividendo; e, fatta la sottrazione, si avrà 0; il quoziente ovvero la parte che toccherà a ciascuno è 23 fr.

Quest'operazione serve di norma a fare le divisioni quando il divisore è contenuto nella prima cifra del dividendo.

D. Come si fa la divisione quando il divisore non può essere contenuto nella prima cifra del dividendo?

R. Quando il divisore non può essere contenuto nella prima cifra del dividendo, allora si prenderanno due cifre. Esempio:

Dividendo	130	5 divisore
	10	26 quoziente
	___
	30
	30
	___
	00

Si dirà: il divisore 5 non istà nella prima cifra del dividendo i, perciò si prenderà anche la cifra seguente che fa 13. Ora il 5 nel 13 entra due volte, si scriva 2 nel quoziente; 2 moltiplicato per 5 dà 10, si scriverà 10 sotto al 13 e si farà la sottrazione; nel resto si opererà come sopra.

D. Come si fa la divisione quando nel divisore vi sono più cifre? {19 [19]}

R. Quando nel divisore vi sono più cifre, si prendono tante cifre nel dividendo quante sono nel divisore, e quando il valore delle cifre del divisore superano quello delle cifre del dividendo si prenderà una cifra di più nel dividendo.

Esempio:

Dividendo	450	25 divisore
	25	18 quoziente
	___
	200
	200
	____
	000

Il 2 che è la prima cifra del divisore sta due volte nella prima cifra del dividendo; ma il 5 che è la seconda cifra del divisore non istà più due volte nel 5 del dividendo, perciò si dirà: il 2 nel 4 sta una volta col residuo di 2 che, uniti al 5, fanno 25. Il 5 del divisore sta anche abbondantemente una volta nel 25; onde si scriverà 1 nel quoziente. Indi si moltiplica il quoziente 1 pel divisore 25, e si avrà per prodotto 25, che si scrive sotto al 45. Fatta la sottrazione si avrà 20 ed accanto di esso si abbasserà l'ultimo 0 del dividendo, per cui risulterà 200. Qui il 25 non potendo essere contenuto in un numero pari di cifre bisognerà prenderne una di più; vale a dire in vece di 20 si prenderà 200, dicendo: il a sta nel 2 del dividendo, ma il 5 non istà più nelle cifre seguenti, perciò si dirà: il 2 nei 20 sta otto volte col residuo di 4 che, unito allo 0, fa 40. Ora il 5 nel 40 sta anche otto volte, e si scriverà 8 nel quoziente, il quale {20 [20]} 8, moltiplicato pel 25, darà 200; fatta poi la sottrazione si avrà 000. Nel quoziente avremo 18.

D. Come si fa la prova della divisione?

R. La prova della divisione si fa moltiplicando il quoziente pel divisore. Se la somma eguaglierà il dividendo l'operazione sarà ben fatta. Esempio:

Dividendo	441	7 divisore
	42	63
	___
	21	7 prova
	21	____
	___	441
	00

Per fare la prova nel proposto esempio si moltiplica il divisore 7 pel quoziente 63; e dando 441, che è somma eguale al dividendo, l'operazione è esatta.

Esercizi sulla divisione.

1. Un signore, mosso da vero spirito di carità, assegna fr. 233 da distribuirsi a 9 povere famiglie. Quanti fr. toccheranno a ciascuna?

2. Un ragazzo generoso vuole regalare 500 noci a 20 suoi compagni; quante ne avrà ciascuno?

3. Un padre di famiglia ha 2190 fr. di reddito annuo; quanto può spendere al giorno onde averne per tutto l'anno ovvero per giorni 365?

Del sistema metrico decimale

D. Che cosa s'intende persistema metrico decimale?

R. Per sistema metrico intendesi il complesso di tutti i pesi e di tutte le misure aventi il metro {21 [21]} per base. Dicesi poi anche decimale perchè si procede sempre per dieci sia nell'aumentare che nel diminuire.

D. Che vuol dire quella parola metro?

R. La parola metro significa misura, ed è lungo 23 oncie 113 del piede liprando. Questo metro è la diecimilionesima parte del quarto del meridiano terrestre, ossia della circonferenza della terra. Vale a dire se intorno alla terra si tirasse un filo, e che questo filo si dividesse in quaranta milioni di parti uguali, una parte formerebbe la lunghezza del metro.

D. Perchè si vuole preferire questo nuovo sistema all'antico che già abbiamo in uso?

R. Per più ragioni, tra cui quella che rende molto più facile il calcolo, ma quello che è più, essendo il metro in tutte le parti del mondo uguale, si eviterà la grande varietà di pesi e di misure che occorrono ne' varii stati, come nel nostro regno, e talora in una medesima provincia. Per questa diversità di pesi e di misure uno va esposto ad errori ed inganni di ogni genere. Il che di leggieri si eviterà in tutti quei luoghi in cui si farà uso del nuovo sistema.

Della numerazione decimale.

D. Quali sono le unità di misura nel sistema metrico decimale?

R. Le unità fondamentali di questo sistema sono sei:

Il metro per le misure di lunghezza.

L'ara per la superficie.

Lo stero pel legno.{22 [22]}

Il litro per le misure di capacità come vino, acqua, grano, meliga e simili.

Il gramma per li pesi.

Il franco per le monete.

D. In vece di quali misure si userà il metro?

R. lo vece del trabucco, del piede e del raso si userà il metro per tutte le misure di lunghezza, come sono tela, panno, strade, e simili.

D. Per misurare i campi, i prati e le vigne si userà anche il metro?

R. Per le misure di superficie ossia dei campi, prati e vigna si usa il metro quadrato, che è uno spazio quadrato lungo, largo un metro. Ma siccome questo spazio sarebbe troppo piccolo per le misure delle campagne, cosi in luogo del metro quadrato venne adottato il decametro quadrato che vale dieci metri in lunghezza e larghezza.

D. Qual nome si dà a questo decametro quadrato?

R. Lo spazio del decametro quadrato venne detto ara, e sì userà in luogo della tavola.

D. L'ara contiene maggiore o minor spazio della tavola?

R. L'ara contiene maggior spazio della tavola e corrisponde a tavole 2, piedi 7, oncie 6.

D. Che cosa intendesi per la parola stero?

R. Stero è un metro cubo, cioè un corpo che ha un metro di spigolo ossia un metro in altezza, lunghezza e larghezza, dicesi stero o metro cubo. Questa misura si userà in luogo della tesa pel fieno, paglia, legna, ghiaia e simili.

D. Che cosa è il litro?

R. Per farti un' idea del litro supponi il metro diviso in dieci parti eguali, avrai un decimetro ossia la decima parte del metro. Ora un decimetro {23 [23]} cubo ossia un vaso lungo, largo, alto un decimetro forma la capacità dei litro.

D. A quale misura verrà sostituito il litro?

R. Il litro verrà sostituito all'emina, al coppo; alla penta ed al boccale. Un terzo del coppo fa un litro, a3 litri fanno un'emina. Il litro corrisponde a tre quartini circa.

D. Che cosa s'intende per gramma?

R. Per gramma s'intende un peso che corrisponde alla trentesima parte dell'oncia. Se tu prenderai il metro e lo dividerai in cento parti eguali, ciascuna di queste parti dicesi centimetro. Ora un centimetro cubo, vale a dire un vaso lungo, largo, alto un centimetro pieno di acqua pura corrisponde al peso del gramma.

D. Come si può dimostrare, che tutte le misure derivino dal metro?

R Essendo il metro la base di tutte le misure decimali è cosa facile il dimostrare come tutte le altre misure da quello derivino.

L'ara, ossia il decametro quadrato altro non è che un quadrato, i cui lati hanno dieci metri di lunghezza.

Lo stero o metro cubo è uguale ad un dado che abbia un metro di spigolo: vale a dire un metro in lunghezza, larghezza e profondità.

Il litro origina dal metro essendo la capacità di un decimetro cubo.

Il gramma vien altresì dal metro, giacchè è il peso di un centimetro cubo d'acqua pura o distillata.

Il franco risulta anche dal metro giacchè pesa cinque grammi, ovvero la sesta parte dell'oncia.

Siccome ciascuna delle unità accennate ha delle variazioni quando si trova minore o maggiore delle {24 [24]} unità medesime; cosi ci sono alcune voci usate in questo sistema che si appellano moltipli quando sono maggiori delle unità; alcune altre si nominano sottomoltipli., quando esprimono solamente parti dell'unità.

D. Quali sono le voci di nomenclatura nel sistema metrico?

R. Le voci di nomenclatura per questo sistema sono sette: quattro si dicono moltipli e servono a nominare l'aumento. Tre appellansi sottomoltipli e servono per dinotare la diminuzione. Le voci di aumento sono:

Deca	che vuol dire	10	unità
Etto	»	100	»
Kilo	»	1000	»
Miria	»	10000	»

I sottomoltipli, ossia le voci di diminuzione, cioè che rendono il valore di dieci in dieci volte minore sono:

Deci	decima	parte dell'unità
Centi	centesima	»
Milli	millesima	»

Il seguente specchio servirà a dilucidare quanto si è detto sopra.

Appellazione scritta	in cifre	in decimale
Unità	1	Unità
Decina	10	Deca
Centinajo	100	Etto
Mille	1000	Chilo
Decina di mila	10000	Miria
Centinajo di mila	100000	Deca-miria
Milione	1000000	Ettomiria

Dal che risulta che una cifra diventa di dieci in dieci volte maggiore a misura che si avanza {25 [25]} di una sede verso sinistra. All'opposto ogni volta che una cifra si avanza di una sede verso la destra diventerà di dieci in dieci volte più piccola. Come:

Unità	1	unità	unità
Decimo	0,1	deci	decima parte dell'unità.
Centesimo	0,01	centi	centes parte »
Millesimo	0,001	milli	milles. parte »
Diecimillesimo	0,0001	decimilli	diecimil parte »
Centomillesimo	0,00001	centimilli	centomil parte »
Milionesimo	0,000001	milli	milli milliones parte »

D. Che cosa bisogna specialmente notare nello scrivere i numeri decimali?

R. Si deve notare diligentemente che gli interi si separano sempre dalle frazioni per mezzo di una virgola, p. e. se io voglio scrivere 25 franchi, più 50 centesimi, dovrà scrivere 25, 50.

Tavola. De' nuovi pesi e delle nuove misure che verranno sostituite ai pesi ed alle misure del sistema antico.

SISTEMA ANTICO

Monete.

Cinque lire fanno uno scudo.

Soldi 20 fanno un franco.

Dodici danari fanno un soldo.{26 [26]}

SISTEMA NUOVO

Monete.

Cinque franchi[2] fanno uno scudo.

Centesimi 100 fanno un franco.

Centesimi 5 fanno un soldo.

SISTEMA ANTICO

Pesi

Rubbi 60 fanno una carra.

Libbre 25 fanno un rubbo.

Oncie 12 fanno una libbra.

Ottavi 8 fanno un'oncia.

Danari 3 fanno un ottavo.

Grani 24 fanno un danaro.

SISTEMA NUOVO

Pesi grosi

La tonnellata che vale 100 miriagrammi.

Il quintale che vale 10 miriagrammi.

Il miriagramma che vale 10 chilogrammi.

Pesi ordinarii.

Il chilogramnla che vale 10 ettogrammi.

L'ettogramma che vale 10 decagrammi.

Il decagramma che vale 10 grammi.

Pesi piccoli.

Il gramma.

Il decigramma che vale la decima parte del gramma.

Il centigrauima che vale la Gentes. parte del gramma.

Il milligramma che la millesima parte del gramma. {27 [27]}

SISTEMA ANTICO

Misure di capacità per i liquidi.

Brente 10 fanno una carra.

Pente 36 fanno una brenta.

Boccali 2 fanno una penta.

Quartini 2 fanno un boccale.

Misure per le materie asciutte.

Sacchi 6 fanno una carra.

Emine 5 fanno un sacco.

Coppi 8 fanno un'emina.

Cucchiai 24 fanno un coppo.

SISTEMA NUOVO

Misure per i liquidi e per le materie asciutte.

Il mirialitro che vale lo chilolitri.

Il chilolitro che vale io ettolitri.

Il litro dividesi in decilitri: decima parte del litro.

Centilitri centesima parte del litro.

Millilitro millesima parte del litro.

Il millilitro ed il mirialitro non sono in uso.

SISTEMA ANTICO

Misure lineari.

Trabucchi 800 fanno un miglio.

Piedi liprandi 6 fanno un trabucco.

Oncie 12 fanno un piede.

Punti 12 fanno un' oncia.

Atomi 12 fanno un punto.

Oncie 40 fanno una tesa.

Oncie 14 fanno un raso. {28 [28]}

SISTEMA NUOVO

Misure lineari.

Il miriametro che vale 10 kilometri.

Il chilometro che vale 10 ettometri.

L' ettometro 10 decametri.

Il decametro 10 metri.

10 decimetri fanno un metro.

100 centimetri fanno un metro.

1000 millimetri fanno un metro.

SISTEMA ANTICO

Misure per le legna, fieno, ghiaja e simili.

La tesa cuba di 40 oncie.

SISTEMA NUOVO

Lo stero o metro cubo.

Il decastero, che vale 10 steri.

Il decistero, decima parte dello stero.

Lo stero ha un solo moltiplo ed un solo sottomoltiplo.

SISTEMA ANTICO

Misure per li terreni.

Quattro trabucchi quadrati fanno una tavola.

Cento tavole fanno una giornata.

SISTEMA NUOVO

Misure per li terreni.

L'ara.

L'ettara che vale 100 are.

Il centiara che è la 100 parte dell'ara. {29 [29]}

Misure del tempo.

Giorni 365 e quando,è bisestile 366 fanno un anno.

Giorni 30 fanno un mese.

Giorni 7 fanno una settimana.

Ore 24 fanno un giorno.

Minuti 60 fanno un' ora.

60 secondi fanno un minuto.

Anni 5 fanno un lustro.

Anni 100 fanno un secolo.

Tavola di rapporto del sistema antico col nuovo metrico decimale e viceversa.

Pesi metrici decimali	Pesi antichi
	rub.	lib.	oncie	danari	grani
Unità. Gramma vale	»	»	»	»	18
Unità. Decagramma vale	»	»	»	7	19
Unità. Ettogramma vale	»	»	3	6	1
Unità. Chilogramma vale	»	2	8	12	19
Unità. Miriagramma vale	1	2	1

Pesi antichi.	Pesi nuovi.
	chilog.	ettog.	grammi
Oncia eguale a	»	»	30
Libbra eguale a	»	3	68
Rubbo eguale a	9	2	22

	rub.	lib.	onc.
Un quintale vale	10	21	1
Una tonnellata vale	108	10

Misure per i liquidi.

Unità. Litro vale quasi quartini 3

Unità. Decalitro pente 7, quartini 3

Unità. Ettolitro brente 2, pente 1

Unità. Chilolitro brente 20, pente 10 {30 [30]}

Unità. Un quartino vale centilitri 34, 2

Unità. Penta vale litri 1, centilitri 36, 9

Unità. Brenta vale litri 49, centilitri 28, 4

Misure per le materie asciutte

	emine	coppi	cucchiai
Unità. Litro vale	»	»	8
Unità. Decalitro	»	3	11
Unità. Ettolitro	4	2	18
Unità. Chilolitro	42	3	17

	litri	centilitri
Coppo vale	2	87
Emina vale	23
Sacco vale	115	2

Misure di lunghezza.

	trab.	piedi	oncie	punti
Centimetro eguale a	»	»	»	2
Decimetro eguale a	»	»	2	4
Metro eguale a	»	1	11	4
Decametro eguale a	3	1	5	»
Ettometro eguale a	32	2	7	»
Chilometro eguale a	324	2	1	»
Miriametro eguale a	3244			»

	chilom.	metri	centim.	millim.
Un punto vale	»	»	»	3
Oncia vale	»	»	4	2
Piede vale	»	»	51	4
Trabucco vale	»	3	8	2
Miglio vale	2.469

Siero pel fieno e per le legna.

	tese	piedi	oncie
Uno stero vale	»	»	7 1/2
Decastero	1	4	7

Il decistero che è un decimo dello stero.

La tesa da fieno vale met. 5, 041.

La tesa da legna vale met. 4, 033.

Misure agrarie ossia di campagna.

	giornate	tavole	piedi	oncie
Un'ara corrisponde a	»	2	7	6
Ettara corrisponde a	2	63	1	1

Tavola corrisponde a centiare 38.

Giornata corrisponde ad are 38.

Metri e rasi.

Raso corrisponde a centimetri 59, millimetri 9.

Metro corrisponde a rasi 1, ottavi 5.

Dell'addizione decimale

D. Come si fa l'addizione de' numeri decimali?

R. Si fa come quella de' numeri interi, badando solo di separare gl' interi dalle frazioni con una virgola; e quando dalla colonna delle frazioni si passa a quella delle unità, si portano le decine secondo il solito senza far conto che siano numeri interi o frazioni.

Esempio. Una serva desiderosa di dare un conto esatto al suo padrone ha notato la spesa tic] modo seguente:

	Speso in formaggio lire	3, 75
	Speso in butirro	4, 60
	Speso in riso e vermicelli	9, 87
		_____
	Totale lire	18, 22

{32 [32]}

Si dirà: 7 più 5 danno 12. Si depone 2 e si prosegue: 1 più 8 danno 9, più 6 danno 15, più 7' fanno 22. Deponiamo 2, dietro a cui si scrive una virgola per separare le frazioni, indi si continua: 9 più 2 che si portano danno 11, più 4 danno 15, più 3 fanno 18. Totale 18, 22.

D. Come si fa l'addizione quando occorrono deca, etto, kilo, micia, da sommarsi insieme nella stessa operazione?

R. Questa si può fare facilmente calcolando bene quante unità ciascun numero contenga, e scrivendo le unità e le decine sotto alle cifre corrispondenti Per es. se io debbo sommare 15 unità, più 15 deca: debbo osservare che in 15 unità si contiene un deca, e che in 15 deca ovvero in 15 decine si contengono 150 unità; perciò la cifra 5 del deca vuole essere scritta sotto alla sua corrispondente, che è 1, nella posta delle unità.

Per agevolare questa operazione soglionsi servire di queste lettere iniziali: U. uno, D. deca, E. etto, K. kilo, M. miria. Queste lettere indicano il sito ove si debbono scrivere le colonne de' numeri. Esempio:

M.K.E.D.U.

Quindici unità	15	eguale a	15
Quindici deca	15	eguale a	150
Venticinque etto	25	eguale a	2500
Ottanta kilo	80	eguale a	80000
Nove miria	9	eguale a	90000
	_______		_______
Totale	172,665		172,665

Si osservi solo che l'ultima cifra è quella che dà il nome a tutte le altre, onde nel proposto caso l'ultima cifra 5, esprimendo le unità, darà il {33 [33]} nome di unità a tutte le altre successive, che se l'ultima cifra esprimesse i deca, il totale verrebbe considerato come altrettanti deca.

Esercizi. 1. Un signore desideroso di dispor bene delle sue ricchezze fa testamento e lascia per la ristaurazione di una chiesa II. 2600 c. 85. Per istruzione della gioventò fr. 550 c. 60 annui. Ai poveri fr. 434, 75. Quanto fa in tutto?

2. Un padre facendo economia ha risparmiato in un anno fr. 825 e. 90; suo figlio privandosi di parecchi divertimenti risparmiò fr. 226 c. 31; la madre per sua speciale diligenza, guadagnò fr. 167 e. 42. Quanto hanno risparmiato tra tutti pel bene della famiglia?

Della sottrazione decimale

D. Come si fa la sottrazione dei numeri decimali?

R. La sottrazione dei numeri decimali si fa come quella dei numeri interi, avvertendo solo di separare gl'interi dalle frazioni decimali con una virgola.

	Esempio. Debbo pagare	341,28
	Pago	141,17
	Resta	200,11

Bisogna però osservare che se il sottraendo ed il minuendo non avessero egual numero di cifre nelle frazioni, si supplisce con altrettanti 0. Es. Debbo ricevere fr. 542 in due volte; ora ricevo fr. 240 c. 75. Quanto debbo ancora ricevere?

	542,00 aggiunti due 00
	240,75
	301,25

Esercizi. 1. Un lavorante deve ricevere in fine della settimana fr. 70, ma perché ha perduto {34 [34]} tempo, gli vengono ritenuti fr. 15,50. Quanto porta ancora a casa?

2. Un operaio deve al panattiere fr. 200,20; per ora paga solamente fr. 118 c. 5. Quanto deve ancora pagare?

3. Ho comperato 425 miriagrammi di uva peso brutto: sono da diminuirsi 117 di tara; quanti miriagrammi restano ancora?

Della moltiplicazione dei numeri decimali.

D. Come si fa la moltiplicazione dei numeri decimali?

R. La moltiplicazione dei numeri decimali si fa come quella dei numeri interi, notando solamente: 1.° quando vi sono delle frazioni si separano secondo il solito con una virgola, e si fa la moltiplica come se fossero tutti interi, e nel prodotto si separano tante cifre con una virgola quante erano le frazioni nei due fattori; 2.° quando in uno dei fattori non vi sono interi, si suole scrivere 0, oppure una virgola, per indicare che non ci sono interi, e si fa l'operazione secondo il solito.

Esempio 1.°	Ho comprato di tela metri	120,50
	Ogni metro pag.	3,45
	Si moltiplica	60250
		48200
		36150
	Addizione	415,72,50

Essendo quattro le cifre decimali, saranno separate con una virgola, ed il prodotto sarà 415 fr., più 72 cent. Il resto sarebbero 50 diecimillesimi, i quali nel calcolo ordinario non si contano. {35 [35]}

Esempio 2.°	Miriagrammi	450 di legna
	Ogni miriag. vale.	0,35
	Si moltiplicherà	2250
		1350
	Addizione	____
	Totale fr.	157,50

Esercizi. 1. Un figlio spende ogni settimana in tabacco da fumare 0,80; quanto spende in un anno ovvero in settimane 52?

2. Un giovane riceve dal padre per li suoi minuti piaceri ogni domenica fr. 1,50; egli, morigerato qual è, conserva tutto per comperarsi abiti e darne parte ai poveri; quanto risparmia in un anno?

3. Un agente ha 135 lavoratiti a 15 fr. per settimana ognuno; quanto dovrà pagare in fitte della settimana?

Della divisione dei numeri decimali

D. Come si fa la divisione dei numeri decimali?

R. La divisione dei numeri decimali si fa come quella degli interi se non occorrono frazioni; nel che si deve notare:

1.° Quando il divisore ed il dividendo hanno egual numero di cifre nelle frazioni, si toglie la virgola e si fa l'operazione come se fossero interi.

2.° Qualora il dividendo od il divisore abbiano disugual numero di cifre nelle frazioni, si rendono pari cori altrettanti zero.

3.° Per dividere un numero per 10, per 100, per 1000, non si fa altro che aggiugnere uno zero per dividerlo in dieci, due zeri per dividerlo per cento, tre zeri per dividerlo per mille, ecc. {36 [36]}

Esempio pel 1.° caso. Ho speso fr. 678 c. 75 in 45 ettolitri, più 25 litri; quanto mi costò ogni ettolitro?

Dividendo

67875

4525 Divisore

15 quoziente

Nel proposto esempio fa lo stesso che tino avesse a dividere 67875 per 4525; il 15 sarà il prezzo pii ciascun ettolitro.

Esempio pel 2.° caso. Ho pagato fr. 115 c. 50 per miriag. 5,5 decimi di caffè; quanto mi costò cadun miriag.?

Dividendo

67875

550 Divisore a cui si aggiunge uno 0

21 quoziente

Si aggingne uno 0 perchè le cifre delle frazioni de1 divisore siano pari a quelle del dividendo, e, fatta secondo il solito la divisione, avremo per quoziente 21 che è il prezzo di ciascun miriagramma.

D. Come si fa la divisione quando il dividendo è minore del divisore?

R. Si fa l'operazione secondo il solito mettendo uno zero prima del quoziente per indicare che le cifre non esprimono numeri interi, e si aumenterà il dividendo di uno 0.

Es. Come si dividono 8 franchi tra 10 persone?

Al dividendo si aggiunge 0

10 Divisore

0,8

Lo 0 aggiunto nel dividendo rende il numero dieci volte maggiore, ma il valore è sempre lo stesso, perchè queste nuove parti sono dieci volte più piccole delle prime: vale a dire le unità {37 [37]} coll'aggiunta di uno 0 diventano decimi; aggiungendone un altro avremo centesimi. Perciò nel dividendo in vece di 80 decimi avremo 800 centesimi, ed invece di 8 decimi nel quoziente avremo 80 centesimi.

D. Che cosa si deve fare quando in fine dell'operazione vi rimane un residuo minore del divisore?

R. A questo residuo si aggiugne uno 0 e si avranno decimi. Aggiunto poi un altro 0 si avranno centesimi, e si continua la divisione. Generalmente, quando oltrepassa i centesimi, il residuo si negligenta.

Esempio. Si dividano fr. 20 a 3 operai.

Dividendo

3 Divisore

Si sottrae

6,66

Per ridurlo in dec. si aggiunge	0	20
Si sottrae		18
Per ridurlo a cent. si aggiunge	0	20
Si sottrae		18
Residuo		2

Il quoziente sarà 6,66. Il residuo 2 che sono cent. si potrebbe ridurre a millesimi coll'aggiunta di uno 0 e continuare la divisione; ma per lo più nel calcolo ordinario i millesimi si trascurano.

Esercizi. 1. Un panattiere vende 800 kilogr. di pane per settimana; quanti kilog. vende al giorno?

2. Un mugnaio ha esatto 720 fr. per 28 ettolitri di frumento; quanto risulta per ciascun ettolitro?

3. Un mercante trova in cassa fr. 2345 per aver venduto 200 metri di panno; quanto ha esatto per ciascun metro? {38 [38]}

Tavola. Dei numeri fissi per convertire le misure antiche in misure nuove e reciprocamente colla semplice moltiplicazione

Distinzione delle misure

Fattori o numeri fissi per

Ridure le misure antiche in nuove cioè

Numero di cifre da separare nel prodotto

Fatorii o numeri fissi per

Ridure le misure antiche in nuove cioè

Numero di cifre da separare nel prodotto

Lineari

3,09

,514

1,715

Le miglia in chilom

I trab. in metri

I piedi in metri

Le tese in metri

I rasi in metri

Una

Due

Tre

Una

,324

1,944

,583

1,67

I chilometri in miglia

I metri in trab.

I metri in piedi

I metri in tese

I metri in rasi.

Una

Tre

Due

Di superficie

9,526

,265

,38

I trab. quad. in metri quadrati

I piedi quadrati in metri quad.

Le gior in ettare

Tre

Due

,105

3,779

2,625

I metri quadr. in trab. quadrati

I metri quadrati in piedi quadr.

Le ettare in gior.

Tre

Di solidità

29,401

,136

5,041

4,033

I trabuc. cubi in metri cubi

I piedi cubi in metri cubi

Le tese pel fieno in steri

Le tese per legno in steri

Tre

,034

7,35

,198

,248

I metri cubi in trabuc. cubi

I metri cubi in piedi cubi

Gli steri pel fieno in tese

Gli steri per legna in tese

Tre

Due

Tre

Di capacità

1,15

,23

I sacchi in ettolitri

Le emine in ettolitri

Le brente in ettolitri

Due

Una

,87

4,34

Gli ettolitri in sacchi

Gli ettolitri in emine

Gli ettolitri in brente

Due

Pesi

,9222

,369

,306

I rubbi in miriagrammi

Le libbre in chilogrammi

Le oncie in ettogrammi

Quattro

Tre

1,0853

2,711

3,253

I miriagrammi in rubbi

I chilogrammi in libre

Gli ettogrammi in oncie

Quattro

Tre

{39 [39]}

[Riduzione delle misure antiche in quelle nuove]

Maniera. di ridurre le misure antiche di Piemonte in misure metrico-decimali e reciprocamente, secondo il modulo esposto nella presente tavola.

D. In che maniera le misure del sistema antico si possono ridurre in misure nuove e reciprocamente?

R. Questa riduzione si fa per mezzo della moltiplicazione cercando il numero fisso.

D. Che cosa s' intende per numero fisso?

R. Per numero fisso s' intende il rapporto che passa tra il numero di un sistema coll'altro. Per es. se io voglio cercare il numero fisso, ovvero il rapporto del piede col metro, dirò: il piede eguaglia metri 0,514. Questo 514 (che sono millimetri) è numero fisso, ovvero la relazione di misura col metro. Volendo cercare il rapporto del metro coi piede dirò: il metro eguaglia piedi 1,944, vale a dire il metro vale un piede più novecento quarantaquattro millesime parti del piede. li numero 1,944 è numero fisso.

D. Dato il numero fisso, come si riducono le misure di un sistema nelle misure dell'altro?

R. Dato il numero fisso si può ridurre le misure di un sistema nell'altro colla moltiplicazione, moltiplicando i! numero fisso pel numero che si vuol ridurre seguendo in ogni cosa le regole di moltiplica metrico-decimale. Esempio: Quanti metri faranno piedi 45? Operazione:

Numero fisso o moltiplicando	0,514
Numero da ridursi o moltiplicatore	45
	2570
	2056
	23,130

{40 [40]}

Spiegazione. Il numero 514 sono millimetri che formano il valore del piede relativamente al metro; 45 sono piedi da moltiplicarsi pel suo rispettivo numero 514. Nel prodotto si separeranno le tre cifre di frazioni; onde si dirà: 45 piedi fanno 23 metri, più 130 millimetri, ovvero 13 centimetri.

D. Conte si la la prova di queste operazioni?

R. La prova di queste operazioni si eseguisce perfettamente colla regola del 9. Così volendo fare la prova del suddetto esempio si dirà:

Nel moltiplicando: 5 più i dà 6 più 4 fa 10, più di 9 è 1 che si scrive nell angolo superiore a sinistra.

1	0
0	0

Nel moltiplicatore: 4 più 5 fauno 9; più di 9 è 0. Scriviamo 0 nell'angolo inferiore. Quindi si dirà: 0 moltiplicato per 1 dà 0; si scrive 0 nel lato superiore a destra.

Nel prodotto: 2 più 3 fanno 5, più 1 fa 6, più 3 fa 9, più 0 fa sempre 9; più di 9 è 0. L'angolo superiore essendo eguale all'angolo inferiore a destra, l'operazione è esatta.

Riduzione dei piedi piemontesi in metri.

Il piede piemontese è di oncie 12.

D. Qual è il numero fisso per ridurre i piedi piemontesi in metri?

R. Il numero fisso per ridurre i piedi in metri è 514; vale a dire 514 millimetri, perchè cinquecento quattordici millimetri fanno la lunghezza del piede.

Regola. Per ridurre i piedi di Piemonte in metri si moltiplica il numero dei piedi pel fattore 514, che sono millimetri, e, separate dal {41 [41]} prodotto le tre frazioni, ne risulteranno i metri e parti del metro.

Esempio. Abbiansi da ridurre 75 piedi di Piemonte in metri.

Operazione: Fattore	0,514 millimetri
moltiplicato per i piedi	_ 75
	2570
	3598
Prodotto	38,550

Separate tre cifre nel prodotto avremo 38 metri più 550 millimetri, ovvero 55 centimetri.

Riduzione dei metri in piedi piemontesi.

D. Qual è il numero fisso per ridurre i metri in piedi piemontesi?

R. Il numero fisso per ridurre i metri in piedi piemontesi è 1,944; perchè un metro vale un piede e novecento quarantaquattro millesime parti del piede.

Regola. Per ridurre i metri in piedi si moltiplicano i metri pel numero fisso 1944, e, separate tre cifre dal prodotto, si avrà il numero dei piedi e parti decimali del piede.

Esempio. Quanti piedi equivalgono 48 metri, 83 centimetri.

Operazione: metri	48,83
	1944
	19532
	19532
	43947
	4883
Prodotto	94,92,552

{42 [42]}

Separate tre cifre pel fattore, ed altre due per li 83 centimetri, ne risulteranno 94 piedi, 92552, decimali, poco meno di 95 piedi. Qui si seguono le regole solite della moltiplica decimale, separando cioè tante cifre quante sono le frazioni.

Riduzione dei trabucchi in metri.

D. Qual è il numero fisso per ridurre i trabucchi in metri?

R. Il numero fisso per ridurre i trabucchi in metri è 3,09; perchè il trabucco vale 3 metri, più 09, ovvero nove centimetri..

Regola. Per ridurre i trabucchi in metri si moltiplica il numero dei trabucchi pel fattore 3,09, e, separate dal prodotto due cifre, si avranno i metri e parli dei metro.

Esempio. Sianvi da convertire 13 trabucchi in metri. Si moltiplica il numero dei trabucchi pel fattore 309, e dal prodotto 4017, separate due cifre a destra, si avranno 40 metri e 17 centimetri, pari a 13 trabucchi.

Operazione: Fattore	309
	13
	927
	309
Prodotto	40,17

cioè 40 metri e 17 centimetri.

Riduzione dei metri in trabucchi

D. Qual è il numero fisso per ridurre i metri in trabucchi?

R. Il numero fisso per ridurre i metri in trabucchi è 0,324; perché il trabucco diviso in mille {43 [43]} parti, ce ne vogliono 324 parti per fare la lunghezza di un metro.

Regola. Per convertire i metri in trabucchi si moltiplica il numero dei metri pel fattore 324, e dal prodotto, separate tre cifre, il risultato darà i trabucchi e parti decimali del trabucco.

NB. La separazione di tre cifre ha luogo sempre quando le unità noti sieno accompagnate da frazioni. Nel caso contrario, oltre le cifre del fattore, devonsi separare ancora tutte quelle che sono moltiplicate col fattore o numero fisso.

Esempio. Volendo sapere a quanti trabucchi corrispondano 40 metri e 17 centimetri, si moltiplica 4017 pel numero fisso 324, e dal prodotto 1301508, se si separano cinque cifre, cioè 3 pel fattore, e due per i 17 centimetri moltiplicati, si otterranno 13 trabucchi, 01508 parti decimali del trabucco, che qui si possono trascurare per essere di poco rilievo.

Operazione: Metri	40,17
Moltiplicati pel fattore	324
	16068
	8034
	12051
Prodotto	13,01,508

cioè 13 trabucchi rispondenti a 40 metri e 17 centimetri.

Misure itinerarie o di lunghezza.

Riduzione delle miglia di Piemonte in chilometri.

D. Qual è il numero fisso per ridurre le miglia in chilometri? {44 [44]}

R. Il numero fisso ovvero il fattore, per ridurre le miglia (di 800 trabucchi) in chilometri, e 2,5; due interi e cinque decimi del kilom., perchè la lunghezza del miglio equivale a due chilometri e mezzo ovvero cinque decimi.

Regola. Per convertire le miglia in chilometri basterà moltiplicare il numero delle miglia pel fattore o numero fisso 25, e dal prodotto, separata una cifra a destra, si avranuo i chilometri e decimali.

Operazione: Miglia.	50
Moltiplicate pel fattore	25
	250
	100
Prodotto	125,0

cioè 125 chilometri, pari a 50 miglia.

Riduzione dei chilometri in miglia di Piemonte.

D. Qual è il onitero fisso per ridurre i chilometri in miglia?

R. Il numero per ridurre i chilometri in miglia è 0.4, perchè 4 decimi del miglio formano la lunghezza di un chilometro.

Regola. Per ridurre i chilometri in miglia di Piemonte si moltiplica il numero dei chilometri pel fattore 4, e, separata nel prodotto una cifra, si otterranno le miglia e parti decimali del miglio.

Esempio. Da Torino in Aosta vi sono 125 chilometri; quante miglia ci sono? Si moltiplica 125 per 4, e dal prodotto 500 si separi lo zero a destra, rimarranno 50 che sono le Miglia cercate. {45 [45]}

Operazione: Chilometri	125
Moltiplicati pel fattore	,4
Prodotto	50,0

cioè 50 miglia, corrispondenti a 125 chilometri.

Riduzione dei metri in tese.

D. Qual è il numero fisso per ridurre i metri in tese?

R. Il numero fisso per ridurre i metri in tese è 0.583; perchè la tesa divisa in mille parti ce ne vogliono 583 per formare la lunghezza di un metro.

Regola. Per ridurre i metri in tese si moltiplicano i metri pel fattore 583, e, separate tre cifre dal prodotto, si otterranno le tese e frazioni.

Esempio. A quante tese corrispondono 15 metri, 435 millimetri?

Operazione: Metri	15,435
	583
	46305
	123480
	77175
Prodotto	8,998,605

Separate tre cifre pel fattore, ed altre tre per li 435 millimetri, resteranno 8 tese, 998605 decimali, poco meno di 9 tese.

Riduzione delle tese in metri.

D. Qual è il numero fisso per ridurre le tese in metri?

R. Il numero fisso per ridurre le tese in metri è 1,715, perchè la tesa vale un metro pit 715 millimetri. {46 [46]}

Regola. Per ridurre le tese in metri si moltiplicano le tese pel fattore 1715, il prodotto, separate tre cifre, darà i metri e parti del metro.

Esempio. Sianvi da convertire 9 tese in metri.

Operazione: Metri	1,715
Moltiplicati per le tese	9
Prodotto	15.435

Separate 3 cifre nel prodotto, ne risulteranno 15 metri, 435 millimetri, equivalenti a 9 tese.

Riduzione dei rasi in metri.

D. Qual è il numero fisso per ridurre i rasi in metri?

R. Il numero fisso per ridurre i rasi in metri è 0,6; perchè 6 decimetri equivalgono alla lunghezza dei raso.

Regola. Per ridurre i rasi in metri basterà moltiplicare il raso pel numero fisso 6, e, separata una cifra nel prodotto, si avranno i metri e parti del metro.

Esempio. Rasi 85 a quanti metri corrispondono?

Operazione: Rasi	85
Moltiplicati pel fattore	0,6
Prodotto	51,0

Separata una cifra nel prodotto, si avranno 51 metri, eguali a 85 rasi.

Riduzione dei metri in rasi.

D. Qual è il numero fisso per ridurre i metri in rasi?

R. Il numero fisso per ridurre i metri in rasi è 1,67; perchè il metro vale un raso, più sessantasette centesimi del raso. {47 [47]}

Regola. Per avere i rasi dai metri conviene moltiplicare i metri pel fattore 167, e, separate due cifre nel prodotto, si otterranno i rasi cercati.

Esempio. A quanti rasi equivalgono 44 metri, 4 decimetri?

Operazione: Metri	44,4
Moltiplicati pel fattore	1,67
	3108
	2664
	444
Prodotto	74,1,48

Separate tre cifre,due pel fattore, ed una per i 4 decimali, si avranno 74 rasi con una piccola frazione che si può abbandonare.

Misure superficiali.

Riduzione dei trabucchi quadr. in metri quadr.

Il trabucco quadrato abbraccia due trabucchi in lunghezza e larghezza.

Il metro quadrato è lo spazio di due metri in lunghezza e larghezza.

D. Qual è il numero fisso per ridurre i trabucchi quadrati in metri quadrati?

R. Il numero fisso per ridurre i trabucchi quadrati in metri quadrati è 9,526; perchè un trabucco quadrato vale 9 metri quadrati, più 526 centimetri quadrati.

Regola Per ridurre i trabucchi quadrati in metri quadrati si moltiplicano i trabucchi pel fattore 9526, e, separate tre cifre nel prodotto, si otterranno i metri e frazioni del metro. {48 [48]}

Esempio. Sianvi trabucchi quadrati 9 da trasformarsi in metri quadrati.

Operazione: Fattore	9,526
Moltiplicato pei trab. quad.	9
Prodotto	85,734

Separate tre cifre, ne risulteranno 85 metri qual., 734 millimetri, eguali a 9 trab. quadr.

Riduzione dei metri quadr. in trabucchi quadr.

D. Qual è il numero fisso per ridurre i metri quadr. in trabucchi quadr.?

R. Il numero fisso per ridurre i metri quadr. in trab. quadr. è 0,105; perchè il trab. quadr. diviso in mille parti, ce ne vogliono 105 per formare un metro quadr.

Regola. Volendosi convertire i metri quadr. in trab. quadr. si moltiplicano i metri pel fattore 105, e, dal prodotto separate tre cifre, si otterranno i trab. quadr. corrispondenti.

Esempio. Veggasi se li 85 metri quadr., 734 decimali qui contro ci restituiscono li 9 trabucchi quadr.

Operazione: Metri quadr.	85,734
Moltiplicati pel fattore.	,105
	428,670
	8573,40
	9,002,070

Separate tre cifre pel fattore ed altre 3 per la frazione 734, ne risulteranno 9 trab. quadr. con una piccola frazione da non farsene caso. {49 [49]}

Riduzione dei piedi quadrati in metri quadrati.

D. Qual è il numero fisso per ridurre i piedi quadrati in metri quadr.?

R. li numero fisso per ridurre i piedi quadrati in metri quadr. è 0,265. Questo 265 sono centimetri, perchè 265 centimetri quadr. formano un piede quadr.

Regola. Per trasformare i piedi quadr. in metri quadr. si moltiplicano i piedi quadr. pel numero fisso 265, e, separate tre cifre dal prodotto, se ne ricaveranno i metri quadr. e frazioni decimali.

Esempio. Quanti metri quadr. si avranno da 35 piedi?

Operazione: Fattore.	,265
Moltiplicato per li piedi quadr.	35
	1325
	795
Prodotto	9,275

Separate tre cifre nel prodotto, ne risulteranno 9 metri quadrati, e 275 decimali, equivalenti a 35 piedi quadr.

Riduzione dei metri quadrati in piedi quadrati.

D. Qual è il numero fisso per ridurre i metri quadrati in piedi quadrati?

R. Il numero fisso per ridurre i metri quadrati in piedi quadrati è 3,779; perchè il metro quadrato vale piedi 3, più 779 millesime parti del piede.

Regola. Per ridurre i metri quadrati in piedi quadrati si moltiplicano i metri pel fattore 3779, e dal prodotto, separando tre cifre, si avranno i piedi quadrati e parti decimali. {50 [50]}

Esempio. Quanti piedi quadrati si otterranno con 9 metri quadrati e 275 frazioni decimali?

Operazione. Metri quadrati.	9,275
Moltiplicati pel fattore.	3,779
	83475
	64925
	64925
	27825
Prodotto	35,050,225

Si separino sei cifre, 3 pel fattore e 3 per la frazione 275, rimarranno 35 piedi con una piccola frazione.

Misure agrarie

Riduzione delle giornate in ettare.

D. Qual è il numero fisso per ridurre le giornate (di 100 tavole) in ettare?

R. E 0,38; perchè la giornata corrisponde ad ettare 0, are 38.

Regola. Per convertire le giornate in ettare si moltiplicano le giornate pel fattore 38, e, separate due cifre, se ne otterranno le ettare.

Esempio. A quante ettare rispondono 34 giornate?

Operazione: Fattore.	,38
Moltiplicato per le giornate.	34
	152
	114
Prodotto	12,92

Cioè 12 ettare, 92 are, eguali a 34 giornate. {51 [51]}

Riduzione delle ettare in giornate.

D. Qual è il numero fisso per ridurre le ettare in giornate?

R. È 2,625; perchè 2 giornate, più 625 millesimi della giornata fanno un' ettara.

Regola. Volendo ridurre le ettare in giornate si moltiplicano le ettare pel fattore 2625, e, separate tre cifre, si trovano le giornate e frazioni.

Esempio. Cercasi se le 12 ettare, 92 are qui contro, restituiscano le 34 giornate.

Operazione: Fattore.	2,625
Moltiplicato per le ettare.	1292
	5250
	23625
	5250
	2625
Prodotto	33,91,500

Separate cinque cifre, cioè tre pel fattore e due per le 92 are, si avranno le 34 giornate con un piccolo svario.

Misure di solidità

Riduzione dei trabucchi cubi in metri cubi.

Il trabucco cubo vale un trabucco in altezza, larghezza e lunghezza.

Il piede cubo vale un piede in altezza, lunghezza e larghezza.

Parimenti il metro cubo vale un metro in altezza, lunghezza e larghezza.

D. Qual è il numero fisso per convertire i trabucchi cubi in metri cubi? {52 [52]}

R. Il numero fisso è 29,401; perchè il trabucco cubo corrisponde a metri cubi 29, più 401 millimetri.

Regola. Per convertire i trabucchi cubi in metri cubi si moltiplicano i trabucchi pel fattore 29,401, e, separate nel prodotto tre decimali, si avranno nel risultato i metri cubi cercati.

Esempio. A quanti metri cubi equivalgono 8 trabucchi cubi?

Operazione: Numero fisso	29 401
Moltiplicato per trab. cubi	8
	_______
Prodotto	235,208

Separate tre cifre nel prodotto si troveranno 135 metri cubi, 208 decimetri cubi.

Riduzione dei metri cubi in trabucchi cubi.

D. Qual è il numero fisso per ridurre i metri cubi in trabucchi cubi?

R. E 0,034; perchè il metro cubo vale trabucchi 0,034, cioè 34 millesime parti del trabucco cubo corrispondono ad un metro cubo.

Regola. Per avere dai metri cubi i trabucchi si moltiplicano i metri per 34, e, separate tre cifre nel prodotto, si avranno i trabucchi cubi cercati.

Esempio. Quanti trabucchi cubi daranno li 235 metri cubi, 208 decimetri cubi?

Operazione: Metri cubi	235,208
Moltiplicati pel fattore	0,34
	______
	940832
	705624
Prodotto	7.997072

{53 [53]}

Separate tre cifre pel fattore, e tre altre per le frazioni 208, si otterranno 7 trabucchi cubi, 997,072 decimali, cioè poco meno di 8 trabucchi.

Riduzione dei piedi cubi in metri cubi.

D. Qual è il numero fisso per convertire i piedi cubi in metri cubi?

R. E 0,136; perchè 136 decimetri cubi corrispondono ad un piede cubo.

Regola. Per ridurre i piedi cubi in metri cubi si moltiplicano i piedi pel fattore 136, e si separano tre cifre nel prodotto.

Esempio. Abbiansi da ridurre 30 piedi cubi in metri cubi.

Operazione: Fattore	0,136
Moltiplicato per piedi cubi.	30

Prodotto	4,080

Separate tre cifre, si avranno 4 metri cubi, 080 parti del metro cubo, equivalenti a 30 piedi cubi.

Riduzione dei metri cubi in piedi cubi.

D. Qual è il numero fisso per convertire i metri cubi in piedi cubi?

R. E 7,35; perchè 7 piedi, più 35 centesimi del piede cubo, corrispondono ad un metro cubo.

Regola. Per ridurre i metri cubi in piedi cubi si moltiplicano i metri pel fattore 735, e si separano nel prodotto due cifre.

Esempio. Cercasi se 4 metri cubi, 080 decimetri cubi ci restituiscano li 30 piedi cubi. {54 [54]}

Operazione: Metri cubi	4,080
Moltiplicati pel fattore	7,35
	20400
	12240
	28560
Prodotto	29,988,00

Separate cinque cifre, due pel fattore e tre per le frazioni 080, si avranno 29 piedi cubi, 98800 decimali, cioè poco meno di 30 piedi cubi.

Riduzione delle tese cube pel fieno in steri o metri cubi.

La tesa cuba vale una tesa ovvero oncie 40 in altezza, lunghezza e larghezza.

D. Qual è il numero fisso per convertire le tese cube pel fieno in steri o metri cubi?

R. E 5.041; perchè la tesa cuba contiene steri 5,041 millimetri cubi.

Regola. Moltiplicato il numero delle tese cube pel fattore 5041 si avranno nel prodotto gli steri o metri cubi.

Esempio. Quanti steri si avranno con tese 18?

Operazione: Numero fisso	5,041
Moltipl. per le tese cube	18
	40328
	5041
Prodotto	90,738

Separate tre cifre, ne risultano 90 steri, 738 decisteri, eguali a 18 tese. {55 [55]}

Riduzione delle tese cube per le legna in ster o metri cubi.

D. Qual è il numero fisso per ridurre le tese cube per le legna in eteri o metri cubi?

R. E 4,033; perchè la tesa cuba per le legna vale steri 4,033 millimetri cubi.

Regola. Per ridurre le tese cube in steri o metri cubi si moltiplicano le tese per il fattore 4033, ed il risultato darà gli eteri cercati.

Esempio. A quanti steri corrispondono 24 tese cube di legna?

Operazione: Numero fisso	4,033
Moltipl. per le tese	24
	16132
	8066
	96,792

Separate tre cifre, si avranno 96 steri, 792 decisteri, equivalenti a 24 tese cube.

Riduzione degli sieri o metri cubi pel fieno in tese cube.

D. Qual è il numero fisso per ridurre gli steri o metri cubi pel fieno in tese cube?

R. E 0,198; perché 198 millesimi (circa un quinto) della tesa cuba da fieno corrisponde ad uno stero o metro cubo.

Regola. Per convertire gli steri in tese cube si moltiplicano gli steri pel fattore 198, e si separano nel prodotto tre decimali.

Esempio. Quante tese cube si otterranno con steri 90,738? {56 [56]}

Operazione: Steri o metri cubi	90,738
Moltiplicati, pel fattore	,198
	725904
	816642
	90738
Prodotto	17.966,124

Separate tre cifre pel numero fisso, e le altre tre per la frazione 738, si avranno 17 tese, 966124 decimali, cioè poco meno di 18 tese.

Riduzione degli sieri o metri cubi per le legna in tese cube.

D. Qual è il numero fisso per convertire gli steri o metri cubi per le legna in tese cube?

R. E 0,248, perchè lo stero per le legna contiene tese cube 0,248 millesimi, cioè un quarto di tesa da legna.

Regola. Per convertire gli steri in tese cube si moltiplicano gli steri col fattore 248, e dal prodotto separando tre cifre, troveremo le tese cube e decimali.

Esempio. Quante tese cube si avranno con steri 96,792?

Operazione: Steri o metri cubi	96,792
Moltiplicati pel fattore	248
	774336
	387168
	193584
Prodotto	24,004,416

{57 [57]}

Fatta la separazione delle tre cifre pel fattore, e di altre tre per i. decimali 792, si avranno 24 tese cube come sopra.

Misure di capacità per le materie asciutte e pei liquidi.

Riduzione dei sacchi in ettolitri.

D. Qual è il numero fisso per ridurre i sacchi in ettolitri?

R. E 1,15; perchè 1 ettolitro, più 15 litri, ovvero 115 litri corrispondono al sacco.

Regola. Per avere il ragguaglio dei sacchi in ettolitri si moltiplicano i sacchi pel fattore 115, ed il prodotto, separato da due cifre, darà la conversione cercata.

Esempio. Sacchi 31 a quanti ettolitri corrispondono?

Operazione: Fattore	1,15
Moltipl. pei sacchi.	31
	115
	345
Prodotto	35.65

cioè 35 ettolitri, 65 litri, eguali a 31 sacchi.

Riduzione degli ettolitri in sacchi.

D. Qual è il numero fisso per ridurre gli ettolitri in sacchi?

R. È 0.87; perchè il sacco diviso in cento parti ce ne vogliono 87 per fare un ettolitro.{58 [58]}

Regola. Per ridurre gli ettolitri in sacchi si moltiplicano gli ettolitri pel fattore 87, e, separate due cifre nel prodotto, si avrà i1 numero cercato dei sacchi.

Esempio. Quanti sacchi valgono ettolitri 35,65?

Operazione: Ettolitri	35,65
Moltipl. pel fattore	87
	24955
	28520
Prodotto	31,01,55

cioè sacchi 31, trascurando il piccolo avanzo.

Riduzione delle emine in ettolitri.

D. Qual è il numero fisso per ridurre le emine in ettolitri?

R. E 0,23; perchè 23 litri corrispondono all'emina.

Regola. Per convertire le emine in ettolitri si moltiplicano le emine pel fattore 23, e si separano due cifre nel prodotto.

Esempio. Qual è il ragguaglio di 40 emine in ettolitri?

Operazione: Emine	40
Moltipl. pel fattore	,23
	120
	80
Prodotto	9,20

Separate due cifre, ne risultano 9 ettolitri, corrispondenti a 40 emine. {59 [59]}

Riduzione degli ettolitri in eroine.

D. Qual è il numero fisso per ridurre gli ettolitri in emine?

R. E 4,34; perchè l'ettolitro vale emine 4, più 34 centesimi dell' emina, ovvero un terzo.

Regola. Per ridurre gli ettolitri in emine si moltiplica il numero degli ettolitri pel fattore 434, e, separate due cifre, si avrà la cercata conversione.

Esempio. A quante emise equivalgono 9 ettolitri e 20 litri?

Operazione: Fattore o numero fisso	4,34
Moltiplicato per gli ettolitri	9,20
	8680
	3906
Prodotto	39,92,80

Separate quattro cifre, due per il fattore e due per li 20 litri, ne risultano 39 emine, 9280 decimali, poco meno di 40 emine.

Riduzione delle brente in ettolitri.

D. Qual è il numero fisso per ridurre le brente in ettolitri?

R. E 0,5; perché 5 decimi dell'ettolitro ovvero 5 decalitri fanno una brenta.

Regola. Per ridurre le brente in ettolitri si moltiplicano pel numero fisso 5, e, separata una cifra nel prodotto, si otterranno gli ettolitri, oppure prendasi la metà delle brente, si avranno subito gli ettolitri; il che si può fare mentalmente il più delle volte senza dar di piglio alla penna. {60 [60]}

Esempio. A quanti ettolitri corrispondono 19 brente?

Operazione: Numero delle brente	19
Moltiplicato pel fattore	,5
Prodotto	9,5

cioè 9 ettolitri, 5 decalitri, ossia 9 ettolitri e mezzo, eguali a 19 brente.

Riduzione degli ettolitri in brente.

D. Qual è il numero fisso per convertire gli ettolitri in brente?

R. E 2; perchè 2 brente fanno un ettolitro.

Regola. Per aver le brente dagli ettolitri si moltiplicano gli ettolitri pel fattore 2, e il prodotto darà le brente cercate, oppure si raddoppia il numero degli ettolitri, ed il risultato sarà lo stesso.

Esempio. Quante brente vagliono li 9 ettolitri, 5 decalitri?

Operazione: Ettolitri	9,5
Moltiplicati pel fattore	2
Prodotto	19,0

Separato lo zero con una virgola per li 5 decalitri, si avranno le 19 brente.

Operazione mentale: Prima volta	9,5
Seconda volta	9,5
Prodotto	19,0

oppure due volte 9, 5, o due volte 9 e mezzo fauno 19 brente. {61 [61]}

Pesi.

Riduzione. dei rubbi in miriagrammi.

D. Qual è il numero fisso per convertire i rubbi in miriagrammi?

R. È 0,9222; perchè 9222 grammi corrispondono al peso del rubbo.

Regola. Per ridurre i rubbi in miriagrammi si moltiplicano i rubbi pel fattore 9222, e dal prodotto, separate quattro cifre si ottengono i miriagrammi cercati.

Esempio. Quanti rubbi valgono 41 miriagram., 4990 grammi, e più facilmente 41 miriagr., 50 ettogrammi?

Operazione: Numero fisso	9222
Moltiplicato per i rubbi	45
	46110
	36888
Prodotto	41,4990

cioè 41 miriagrammi, 49 ettogrammi, 9o grammi, oppure 41 miriagrammi, 4990 grammi, eguali a 45 rubbi.

Riduzione dei miriagrammi in rubbi.

D. Qual è il numero fisso per ridurre i miriagrammi in rubbi?

R. È 1,0843; perchè rubbi 1,0843 diecimillesimi del rubbo fanno un miriagramma.

Regola. Per ridurre i miriagrammi in rubbi si moltiplicano i miriagrammi pel fattore 1,0843, e, separate nel prodotto. quattro cifre, ne risultano i rubbi e parti decimali del rubbo. {62 [62]}

Esempio. A quanti miriagrammi corrispondono 45 rubbi?

Operazione: Fattore	1,0843
Moltiplicato per miriag.	41,50
	542150
	10843
	43372
Prodotto	44,99,8450

Separate quattro cifre pel fattore e due altre per la frazione 50, si avranno poco meno di 45 rubbi.

Riduzione delle libbre in kilogrammi.

D. Qual è il numero fisso per convertire le libbre in kilogrammi?

R. E 0,369; perchè 369 grammi corrispondono alla libbra.

Regola. Per convertire le libbre in kilogrammi si moltiplicano le libbre pel fattore 369, e, separate tre cifre nel prodotto. si otterranno i kilogrammi cercati.

Esempio. Quanti kilogrammi valgono 30 libbre?

Operazione: Fattore	,369
Moltiplicato per le libbre	30
Prodotto	11,070

cioè 11 kilogrammi, 070 grammi, eguali a 30 libbre.

Riduzione dei kilogranmi in libbre.

D. Qual è il numero fisso per ridurre i kilogrammi in libbre?

R. E 2,711; perchè libbre 2, più 711 millesimi della libbra fanno un kilogramma.

Regola. Per convertire i kilogrammi in libbre {63 [63]} si moltiplicano i kilogrammi pel fattore 2711, e, separate tre cifre, si avranno le libbre cercate.

Esempio. A quante libbre equivalgono 11 kilogrammi, 070 grammi?

Operazione: Kilogrammi	11,070
Moltiplicati pei fattore	2,711
	11070
	11070
	77490
	22140
Prodotto	30,010.770

Separate tre cifre pel fattore e tre altre per la frazione 070, ne risultano 30 libbre con un piccolo avanzo.

Riduzione delle oncie in ettogrammi.

D. Qual è il numero fisso per ridurre le oncie in ettogrammi?

R. È 0,307; perchè 307 decigrammi corrispondono al peso dell'oncia.

Regola. Per convertire le oncie in ettogrammi si moltiplicano le oncie pel numero fisso 307, e, separate nel prodotto tre cifre, ne risulteranno gli ettogrammi e frazioni decimali.

Esempio. 18 oncie a quanti ettogrammi corrispondono?

Operazione: Fattore o numero fisso	,307
Moltiplicato per le oncie	18
	2456
	307
Prodotto	5,526

{64 [64]}

cioè 5 ettogrammi, 52 grammi, 6 decigrammi, oppure 5 ettogrammi, 63 grammi, equivalenti a 18 oncie.

Riduzione degli ettogrammi in onde.

D. Qual è il numero fisso per convertire gli ettogrammi in oncie?

R. E 3,253; perchè l'ettogramma fa oncie 2, più 253 millesimi (un quarto) dell'oncia.

Regola. Per ridurre gli ettogrammi in oncie si moltiplicano gli ettogrammi pel fattore 3253; si avrà col prodotto le oncie cercate, previa la separazione di tre decimali.

Esempio. Gli ettogrammi 5, 526 decigrammi, a quante oncie corrispondono?

Operazione: Ettogrammi	5,526
Moltiplicati pel fattore	3,253
	16578
	27630
	11052
	16578
Prodotto	17,976,078

Separate sei cifre, tre pel fattore e tre per la frazione 526, ne risultano 17 oncie, 976078 decimali, cioè poco meno di 18 oncie. {65 [65]}

Dialoghi. Intenti a facilitare la riduzione delle antiche isure in nuove metrico-decimali e reciprocamente, ricavate dalla Metrologia comparata del Milanesio.

Misure metriche lineari e loro rapporto colle misure di Piemonte.

D. Che cosa è il metro?

R. Il metro è la quaranta millionesima parte dei meridiano terrestre, ossia della circonferenza della terra. Supponi un filo che giri tutto intorno alla terra, se tu dividerai questo filo in quaranta milioni di parti eguali, una parte forma la lunghezza del metro.

D. A quale misura piemontese corrisponde il metro?

R. Il metro equivale 1 piede, 11 oncie 173, ossia 1 piede e 944 millesime parti del piede piemontese o liprando.

D. Qual è il ragguaglio del metro alla tesa di 40 oncie?

R. Il metro vale 583 millesime parti della tesa, quasi 6 decimi della tesa.

D. Qual è l' unità di misura lineare, di tracciatura o da panno?

R. Il metro.

D. Qual è il ragguaglio del metro al raso?

R. Il metro vale 1 raso, 60 centesimi di raso (1 raso 273).

D. Se il metro contiene un raso 273, a quanti rasi corrispondono metri 21?

R. Aggiungo al numero 21 i due terzi che sono 7, più 7, eguale a 14, avrò nel totale 35, il numero dei rasi eguali a 21 metri. {66 [66]}

D Qual è l'unità delle misure itinerarie?

R. Il chilometro, e per le grandi distanze il e miriametro.

D. A quante miglia di Piemonte, di 800 trabucchi, equivale il chilometro e a quante il miriametro?

R. Il chilometro vale 324 trabucchi, cioè 275 di miglio, ed il miriametro vale miglia 4,1720, ma si ritiene che cinque chilometri, ossia un mezzo miriametro, fanno 2 miglia.

D. Se un chilometro vale 275 di miglio, cioè quattro decimi di miglio. sarà facile di trovare, senza dar di piglio alla penna, il numero delle miglia di Piemonte, per esempio da Torino a Rivoli, la cui distanza è 12 chilometri e mezzo?

R. Moltiplico per i 4 decimi, cioè per 4 172 chilometri, e trovo che 4 volte 12 172 fanno 50; separo lo zero, e mi resterà il 5, che saranno cinque miglia, corrispondenti ai 12 chilometri e mezzo.

D. Seguendo la stessa regola di operazione mentale, ditemi quante miglia vi sono da Torino a Susa, sapendo esservi una distanza di 55 chilometri?

R. Moltiplicando 55 per 4 avrò 220, e togliendo lo zero, mi rimarranno 22, che saranno le 22 miglia ricercate.

D. Che cosa vogliono esprimere i vocaboli deci, centi, milli?

R. Deci vuoi dire un decimo di un'unità; centi un centesimo; milli un millesimo.

D. Che cosa vogliono significare i vocaboli deca, etto, chilo, miria?

R. Deca vuol dire una decina di unirà; etto un centinaio; chilo un migliaio; e micia una decina di migliaia. {67 [67]}

D. A che cosa servono i vocaboli deca, etto, chilo, micia?

R. Servono per formare i moltipli ossiano le misure maggiori delle unità colla stessa progressione decimale.

D. Che differenza vi passa tra il vocabolo deci ed il vocabolo deca?

R. Deci significa il decimo dell'unità, e deca esprime dieci volte l'unità.

MISURE LINEARI DI PIEMONTE.

D. Ditemi il ragguaglio del trabucco di sei piedi piemontesi al metro?

R. Il trabucco vale 3 metri, 086 millimetri.

D. Ditemi il ragguaglio del piede piemontese al metro?

R. Il piede piemontese (di 12 oncie) vale metri 0,514 millimetri.

D. A quanti metri corrisponde la tesa di 40 oncie?

R. La tesa vale 1 metro, 577 del metro, cioè i metro, 715 millimetri.

D. Ditemi il ragguaglio del raso al metro?

R. Il raso di Piemonte (14 oncie) vale 375 del metro, cioè 6 decimetri.

D. Un miglio di Piemonte a quanti chilometri equivale?

R. Il miglio vale 2 chilometri, 469 metri; ma si ritiene per 2 chilometri e mezzo.

D. Un'oncia del piede piemontese quanti centimetri vale?

R. L'oncia corrisponde a 4 centimetri, ma si ritiene che 7 oncie fanno precisamente 3 decimetri ossiano 30 centimetri. {68 [68]}

MISURE METRICHE SUPERFICIALI.

D. L'ara, che vale 100 metri quadrati, unità principale della misura agraria, a quante tavole di Piemonte corrisponde?

R. L'ara vale 2 tavole e 578 di tavola, ossia 2 tavole, 7 piedi, 5 oncie.

D. L'ettara a quante giornate di Piemonte equivale?

R. L'ettara vale 2 giornate e 578 di giornata di terreno, ossia 2 giornate, 68 tavole, 5 piedi.

D. Il metro quadrato a quanti trabucchi quadrati corrisponde?

R. Il metro quadrato vale 105 millesime parti del trabucco quadrato.

D. Il metro quadrato quanti piedi piemontesi contiene?

R. Il metro quadrato contiene 3 piedi quadrati e 779 millesime parti del piede quadrato.

MISURE SUPERFICIALI DI PIEMONTE.

D. Datemi il ragguaglio della giornata di terreno di 100 tavole in misura superficiale metrica?

R. La giornata vale 38 are.

D. La tavola a quanto equivale?

R. La tavola vale 38 centiare.

D. Qual è il ragguaglio. del trabucco quadrato al metro quadrato?

R. Il trabucco quadrato vale metri quadrati 9,52 decimetri quadrati.

D. Il piede piemontese quadrato quanto vale?

R. Il piede piemontese quadrato risponde a 26 decimetri quadrati.

D. Il piede di trabucco quadrato a quanti metri quadrati corrisponde? {69 [69]}

R. Il piede di trabucco quadrato è eguale a 1 metro, 58 decimetri quadrati.

D. 34 piedi quadrati quanti metri contengono?

R. Contengono 9 metri quadrati.

D. 49 oncie quadrate quanti decimetri quadrati fanno?

R. Fanno g decimetri quadrati.

MISURE METRICHE PER I SOLIDI.

D. Il metro cubo quanti trabocchi contiene?

R. Il metro cubo contiene trabucchi cubi 0,034 millesimi del trabucco.

D. Il metro cubo quanti piedi cubi contiene?

R. Il metro cubo contiene. piedi cubi 7,347 millesimi.

D. Lo stero o metro cubo per i fieni quante tese cube contiene?

R. Lo siero pei fieni contiene tese cube 0,198 millesimi, cioè un quinto di tesa da fieno, cosicchè cinque steri fanno una tesa cuba per la misura dei fieni.

D. Lo stero per le legna quante tese cube contiene?

R. Lo stero per le legna contiene tese cube 0,248 millesimi, cioè un quarto di tesa da legna, cosicchè quattro steri fanno una tesa di legna.

MISURE DI PIESIONTE PEI SOLIDI.

D. Il trabucco cubo quanti metri cubi contiene?

R. Il trabucco cubo contiene metri cubi 29,401 millimetri.

D. Il piede piemontese cubo quanti metri contiene? {70 [70]}

R. Il piede cubo contiene metri cubi 0,136 decimetri cubi.

D. L'oncia di piede cubo quanti metri cubi contiene?

R. L'oncia di piede cubo contiene metri cubi 0,011 decimetri cubi.

D. L'oncia cuba quanti decimetri cubi contiene?

R. L'oncia cuba contiene decimetri cubi 0,078 millimetri.

MISURE METRICHE DI CAPACITÀ PER LE MATERIE ARIDE E PER I LIQUIDI.

D. Il litro per le materie asciutte a quanto equivale in misura di Piemonte?

R. I1 litro contiene 8 cucchiai, 33 centesimi del cucchiaio. 24 cucchiai fanno un coppo.

D. Il litro pei liquidi quanto contiene?

R. Il litro contiene 5 bicchieri, 84 centesimi, cioè 374 di penta.

D. Il decalitro per le materie asciutte quanto contiene?

R. Il decalitro contiene coppi 3, cucchiai 11, e centesimi 28, cioè coppi 3172.

D. Il decalitro pei liquidi quanto contiene?

R. Il decalitro corrisponde a pente 7, bicchieri 2172.

D. L'ettolitro per le materie asciutte a quanto equivale?

R. L'ettolitro equivale a emine 4, coppi 2, cucchiai 16, cioè 4 emine ed un terzo.

D. L'ettolitro per i liquidi a quanto corrisponde?

R. L'ettolitro contiene 2 brente ed 1 penta, ossiano 73 pente; però la brenta si calcola 172 ettolitro (50 litri). {71 [71]}

D. Il chilolitro (metro cubo) pei liquidi quanto contiene?

R. Il chilolitro contiene 20 brente, 10 pente (due carre circa).

MISURE DI CAPACITÀ DEL PIEMONTE.

D. Il. sacco di 5 emine quanti ettolitri contiene?

R. Il sacco contiene 1 ettolitro, 15 litri.

D. L'emina di 8 coppi quanti decalitri e litri contiene?

R. L'emina contiene 2 decalitri, 3 litri, ossia 23 litri.

D. Il coppo di 24 cucchiai quanti litri contiene?

R. Il coppo contiene 2 litri, 9 decilitri, poco meno di 3 litri.

D. La carra di 10 brente quanti ettolitri contiene?

R. La carra contiene 4 ettolitri, 93 litri, poco meno di 5 ettolitri.

D. La brenta di 36 pente quanti litri contiene?

R. La brenta contiene 49 litri e 307 millilitri.

D. La penta di due boccali quanto contiene?

R. La penta è 1 litro, 4 decilitri, ossiano 14 decilitri.

PESI METRICI.

D. Il miriagramma a qual peso di Piemonte corrisponde?

R. Il miriagramma vale 1 rubbo, 2 libbre, 1 oncia (12 miriagrammi fanno 13 rubbi).

D. Il chilogramma a qual peso equivale?

R. Il chilogramma si ritiene eguale a 2 libbre, 8 oncie e mezza, ossiano 32 oncie e mezza. {72 [72]}

D. L'ettogramma quanto vale?

R. L'ettogramma vale 3 oncie e 174.

D. Il decagranima a quanto corrisponde?

R. Il decagramma vale un terzo dell'oncia.

D. Il gramma a che cosa corrisponde?

R. Il gramma corrisponde a 18 grani, e tre quarti di grano.

D. Il quintale metrico o decimale di 100 chilogrammi a quanto equivale?

R. Il quintale metrico o decimale vale 10 rubbi, 21 libbra e 1 oncia.

D. La tonnellata di mare di 1000 chilogrammi quanti rubbi contiene?

R. La tonnellata di mare contiene 108 rubbi, e 10 libbre (peso corrispondente ad un metro cubo d'acqua di mare).

PESI DI PIEMONTE.

D. Il rubbo di 25 libbre quanti chilogrammi vale?

R. Il rubbo vale 9 chilogrammi, 222 grammi.

D. La libbra di 12 oncie a quanti grammi equivale?

R. La libbra vale 369 grammi (19 libbre fanno 7 chilogrammi, e 6 libbre fanno 2 chilogrammi e poco più di un quinto).

D. L'oncia di 8 ottavi quanto vale?

R. L'oncia vale 30 grammi.

D. Il quintale metrico, che pesa 10 rubbi, 21 libbra e 1 oncia, a quanti miriagrammi o chilogrammi corrisponde?

R. Il quintale metrico contiene 10 miriagrammi, ossia 100 chilogrammi. {73 [73]}

D. La tonnellata di mare, che è un peso di 108 rubbi, 10 libbre e 10 oncie, a quanti miriagrammi o chilogrammi equivale?

R. La tonnellata di mare pesa 100 miriagrammi, ussiano 1000 chilogrammi (1 milione di grammi).

Ragguaglio. Di alcuni pesi e di alcune misure paragonate approssimativamente

1 centimetro ha circa la larghezza dell'unghia del dito mignolo.

2 centimetri corrispondono alla grossezza del dito di un uomo.

1 decimetro alla larghezza della mano.

2 decimetri alla spanna ordinaria di un uomo.

1 metro ha 10 volte la larghezza della mano.

1 metro corrisponde ad un lungo passo.

Un uomo con passo ordinario in un minuto percorre i ettometro, in dieci minuti 1 kilometro.

Un cavallo trottando in un'ora può percorrere 10 kilometri. Correndo a gran galoppo può percorrere sino 40 kilometri.

Una vettura a vapore sopra la strada ferrata in un' ora percorre 80 kilometri.

Un moscherino pesa 1 milligramma.

Il peso di un uomo ordinario e' di 65 kilogr.

Un bue od un cavallo di grossezza ordinaria pesa 400 kilogr.

40 pezze da 5 franchi fanno 1 kilogr.

4 pezze di 5 franchi 1 ettogr.

1 pezza da due franchi fa 1 decagramma.

1 pezza da 25 centesimi fa 1 gramma e 174. {74 [74]}

Appendice sulle monete.

Credo far cosa grata al lettore l'aggiugnere qui un'appendice sulle monete più usate tra noi, e sopra le principali monete estere tollerate nei nostri Stati.

D. Che cosa intendesi per monete?

R. Diconsi monete quei pezzi d'oro, d'argento o di rame che servono a valutare il prezzo o d'un oggetto o d'un lavoro.

D. Qual è l'unità delle monete?

R. L'unità delle monete è il franco ovvero la lira nuova che è una moneta per lo più battuta coll'effigie del sovrano, del peso di cinque grammi contenente 9 decimi d'argento ed un decimo di lega o rame.

D. Che differenza passa tra lira e franco?

R. La lira ha un valore variabile secondo viene fissato nei vari stati; per esempio la lira presso noi è di cent. 100; presso i parmigiani è di cent. 85.

Il franco poi è il nome che vuolsi propriamente dare a quella unità metrica, che in ogni tempo, in ogni luogo ha sempre lo stesso valore di venti soldi ovvero cento centesimi.

D. Quali sono le monete specialmente in uso nel nuovo sistema metrico-decimale?

R. La serie delle monete decimali del nostro stato si compone di dodici pezze.

Quattro in oro, cioè da fr. cento, da cinquanta, da venti (marengo) e da dieci.

Cinque in argento, cioè da fr. cinque (scudo), da due, da uno, da cinquanta centesimi, e da venticinque centesimi.

Tre in rame, cioè da cinque centesimi (soldo), da tre, e da uno. {75 [75]}

SPECCHIO DELLE MONETE DECIMALI DELLO STATO

indicante il numero ed il nome delle pezze, il loro diametro e titolo, la tolleranza di peso e di titolo ed il loro valore.

No. delle monete	Nome delle monete	Diametro delle monete	Titolo o valore intrins.	TOLERANZA di titolo per chil.	PESO LEGALE	Toleranza sul peso delle monete	Peso che può avere in più o in meno	TAGLIO al chilograma	VALORE
4 pezze in oro		Millim.	Milles.		Gr.		Milligr.		Fr.
	Pez. da fr. 100	44	900	2/1000	32,2580	1/1000	32	31	100 ,
	» » 50	27	»	»	16,1290	»	16	62	50 ,
	» » 20	21	»	»	6,4516	2/1000	12 ½	155	20 ,
	» » 10	18	»	»	3,2258	»	6 ¼	310	10 ,
5 pezze in argento
	Pez. da fr. 5	37	900	3/1000	25	3/1000	75	40	5 ,
	» » 2	27	»	»	10	5/1000	50	100	2 ,
	» » 1	23	»	»	5	»	25	200	1 ,
	» » 0,50	18	»	»	2,50	7/1000	18	400	0,50 ,
	» » 0,25	15	»	»	1,25	10/1000	12 ½	800	0,25 ,
3 p. in ramo
	Pez. da c. 5	28			10	20/1000	200	100	0,05 ,
	» » 3	23			6	»	120	166	0,03 ,
	» » 1	19			2	»	40	500	0,1 ,

Oro	MONETE ANTICHE DELLO STATO IN CORSO
	Dep di Geneva	.....	905	_____	9,116	Pel la toll. basta che coll’agiunta		...	28,45 ,
	Quadruplo di Geneva	.....	909	_____	25,214	Di 13 milligram. stieno in bilancia		...	79.

{76 [76]}

TARIFFA DELLE MONETE ESTERE

le quali hanno corso nei R. Stati di Terraferma di S. M.

DENOMINAZIONE DELLE MONETE		TITOLO	PESO LEGALE		VALORE
MONETE D'ORO.		mil.	gr.		ll.	c.
Monarchia Austriaca	Doppio Sovrano vecchio	915	11	078	34	81
	Doppio Sovrano nuovo del R. Lomb. Ven	900	11	331	35	02
	Zecchino d'Austria	982	3	452	11	64
	Zecchino d'Ungheria	984	3	452	11	66
	Zecchino di Vienna	997	3	452	11	82
Già regno d’Italia Francia Olanda Parma	(Pezza da lire 20	900	6	452	20	»
	(Pezza da lire 40	900	12	903	40	»
	(Pezza da franchi 20	900	6	452	20	»
	(Pezza da franchi 40	900	12	903	40	»
	Zecchino	978	3	452	11	59
	(Pezza da 20 lire	900	6	452	20	»
	(Pezza da 40 lire	900	12	903	40	»
Portogallo Roma	Doppia	914	28	176	89	70
	Doppia di Pio VI	908	5	430	16	93
	Doppia di Pio VII	898	5	450	16	80
Due Sicilie Spagna Toscana Monarchia Austriaca	Zecchino	995	3	400	11	61
	(NAPOLI; On. di 3 duc. dopo il 1818	996	3	786	12	95
	(SICILIA: Oncia dopo il 1748.	873	4	380	13	10
	(Quadruplo dal 1772 al 1785	894	26	895	82	52
	(Quadruplo dopo il 1785	866	27	045	80	22
	(Ruspone	996	10	406	35	59
	(Zechino	995	3	452	11	79
	MONETE D'ARGENTO
	Tallero d'Austria	831	27	960	5	02
	Crocione delle tre corone	868	29	448	5	56
	Scudone del Regno Lombardo-Veneto	898	25	986	5	10
Francia Parma Spagna Toscana	(Scudo da 5 franchi	900	25	»	5	»
	(Pezza da 2 franchi	900	10	»	2	»
	(Scudo da 5 lire.	900	25	»	5	»
	(Pezza da 2 lire	900	10	»	2	»
	Colonna della Penisola.	896	26	948	5	28
	Francescone o Pisis	916	26	972	5	40

FINE.

{77 [77]}

Indice

Avvertenza	pag. 3
Dialogo	5
Regole per conoscere i numeri	ivi
Esercizi sulla numerazione	6
Dell'addizione	7
Esercizi sull'addizione	9
Della sottrazione	ivi
Esercizi sopra la sottrazione	12
Della moltiplicazione	13
Esercizi sulla moltiplicazione	17
Della divisione	ivi
Esercizi sulla divisione	21
Del sistema metrico decimale	ivi
Della numerazione decimale	22
Tavola de' nuovi pesi e delle nuove misure che verranno sostituite ai pesi ed alle misure del sistema antico	26
Tavola di rapporto del sistema antico col nuovo metrico decina. e viceversa	30
Dell'addizione decimale	32
Della sottrazione decimale	34
Della moltiplicazione dei numeri decimali	35
Della divisione dei numeri decimali	36
Tavola dei numeri fissi	39
Maniera di ridurre le misure antiche di Piem. in misure metrico decimali e reciprocamente	40
Riduzione dei piedi piemont. in metri.	41
Riduzione dei metri in piedi piemont.	42 {78 [78]}
Riduzione dei trabucchi in metri.	43
Riduzione dei metri in trabucchi	ivi
Misure itinerarie o di lunghezza	44
Riduzione delle miglia di Piem. in chilometri	ivi
Riduzione dei chilometri in miglia di Piem.	45
Riduzione dei metri in tese	46
Riduzione delle tese in metri	ivi
Riduzione dei rasi in metri	47
Riduzione dei metri in rasi	ivi
Misure superficiali	48
Riduzione dei trab. quadrati in metri quadrati	ivi
Riduzione dei metri quadrati in trab. quadrati	49
Riduzione dei piedi quadrati in metri quadrati	50
Riduzione dei metri quadrati in piedi quadrati	ivi
Misure agrarie.	51
Riduzione delle giornate in ettare	ivi
Riduzione delle ettare in giornate	52
Misure di solidità	ivi
Riduzione dei trab. in metri cubi	ivi
Riduzione dei metri cubi in trab. cubi	53
Riduzione dei piedi cubi in metri cubi	54
Riduzione dei metri cubi in piedi cubi.	ivi
Riduzione delle tese cube pel fieno in steri o metri cubi	55
Riduzione delle tese cube per le legna in steri o metri cubi	56
Riduzione degli steri o metri cubi pel fieno in tese cube	ivi
Riduzione degli steri o metri cubi per le legna in tese cube.	57
Misure di capacità per le materie asciutte e pei liquidi.	58
Riduzione dei sacchi in ettolitri	ivi
Riduzione degli ettolitri in sacchi	ivi {79 [79]}
Riduzione delle eroine in ettolitri	59
Riduzione degli ettolitri in emine	60
Riduzione delle brente in ettolitri	ivi
Riduzione degli ettolitri in brente	61
Pesi	62
Riduzione dei rubbi in mi miriagrammi	ivi
Riduzione dei miriagrammi in rubbi	ivi
Riduzione delle libbre in kilogrammi	63
Riduzione dei kilogrammi in libbre	ivi
Riduzione delle oncie in ettogrammi	64
Riduzione degli ettogrammi in oncie	65
Dialoghi intenti a facilitare la riduzione delle antiche misure in nuove metrico-decimali e reciprocamente	66
Misure metriche lineari e loro rapporto colle misure di Piemonte » ivi Misure lineari di Piemonte	68
Misure metriche superficiali	69
Misure superficiali di Piemonte	ivi
Misure metriche per i solidi	70
Misure di Piemonte pei solidi	ivi
Misure metriche di capacità per le materie aride e per i liquidi	71
Misure di capacità del Piemonte	72
Pesi metrici	ivi
Pesi di Piemonte	73
Ragguaglio di alcuni pesi e di alcune misure paragonate approssimativamente	74
Appendice sulle monete	75
Specchio delle monete decim. dello Stato.	76
Tariffa delle monete estere, le quali hanno corso nei R. Stati di Terra-ferma di S. M.	77 {80 [80]} {81 [81]} {82 [82]}

[1] Questa regola può patire qualche eccezione riguardo alle frazioni del sistema antico; ma nel nuovo sistema decimale si estende a qualsiasi operazione.

La prova poi della moltiplicazione nel sistema antico, per lo più si faceva col raddoppiare il moltiplicatore, moltiplicandolo secondo il solito pel moltiplicando. In fine si prende la metà del prodotto, il quale se e uguale al prodotto della prima moltiplicazione il calcolo è esatto.

[2] Il vocabolo franco deve preferirsi a lira, perchè la lira nei valore varia nei vari paesi: il franco conserva sempre il medesimo valore.